Grafikus oldatot másodfokú egyenlet

Grafikus oldatot másodfokú egyenlet

A másodfokú egyenlet már találkozott során algebra 7. osztályban. Emlékezzünk, hogy egy másodfokú egyenlet nevezzük egyenlet formájában ax 2 + bx + c = 0, ahol a, b, c - bármilyen számot (arányok), ahol a. Segítségével tudásunk néhány funkciók és grafikonok, képesek vagyunk még most is, anélkül, hogy megvárná a szisztematikus vizsgálata a téma „másodfokú egyenlet” (ez lesz később, a 4. fejezetben), hogy megoldja néhány másodfokú egyenletek, és különböző módon; Úgy véljük, ezek a módszerek a példa egy másodfokú egyenlet.

Példa. Ahhoz, hogy az egyenlet megoldásához x 2 - 2x - 3 = 0.
Határozat.
I. módszer. Ábrázoljuk a függvény az y = x 2 - 2x - 3, használva az algoritmus a 13. §:

1) van egy = 1, b = -2, x0 = 1, y0 = f (1) = 1 2 - 2 - a 3 = -4. Ennélfogva, a csúcsa a parabola egy pont (1; 4) és a parabola tengelye - az egyenes vonal az x = 1.

2) veszi az x-tengely két pont szimmetrikus a parabola tengelyével, például X = -1, és X = 3.

3) Miután a pont (1; 0), (1, -4), (3, 0) lebonyolítása a parabola (lásd 68. ábra) ..

A gyökerei az egyenlet x 2 - 2x - 3 = 0 metszék a parabola metszéspontok az X tengellyel; jelenti a gyökerei az egyenlet x1 = - 1, x 2 - 3.

II módszer. Mi átalakítani az egyenlet, hogy az x 2 = 2x + 3. Beépített egy grafikus koordináta-rendszer funkcióit y - x 2 és y = 2x + 3 (69. ábra). Ezek metszik egymást két pont A (- 1, 1) és B (3; 9). A gyökerek az egyenlet abszcisszái a A és B pontok, akkor X1 = - 1, x 2 - 3.

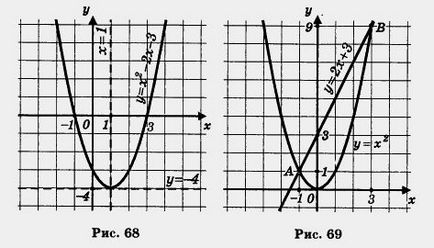
III folyamat. Mi átalakítani az egyenlet, hogy az x 2 - 3 = 2x. Konstrukciót egy grafikus rendszer funkcióit koordináta y = x 2 - 3 és y = 2 (70. ábra). Ezek metszik egymást két pont az A (-1, - 2) és B (3; 6). Vannak a gyökerek a abszcissza A és B pontok, azonban = x1 - 1, x2 = 3.

IV módszer. Transform a egyenlet x 2 -2x 4-1-4 = 0
és további
x 2 - 2x + 1 = 4, azaz a (X - .. IJ = 4.
Készítünk egyetlen koordináta-rendszerben, a parabola y = (X - 1) 2, és a vonal az y = 4 (71. ábra). Ezek metszik egymást két pont az A (-1, 4) és a B (3, 4). A gyökerek az egyenlet abszcisszái a A és B pontok, ezért, x1 = -1, x2 = 3.

V módszer. Termwise elosztva mindkét oldalán x, megkapjuk

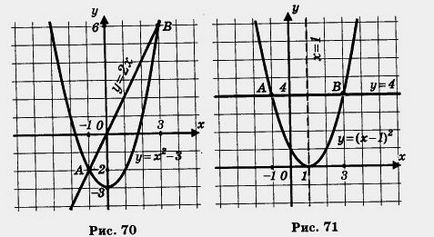
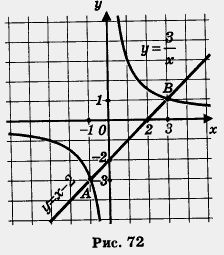
Készítünk egyetlen koordináta-rendszerben, egy hiperbola és egy egyenes vonal y = x - 2 (ábra. 72).

Ezek metszik egymást két pont az A (-1, -3) és B (3, 1). Vannak a gyökerek a abszcissza A és B pontok, ezért, X1 = - 1, x2 = 3.

Tehát a másodfokú egyenlet x 2 - 2x - 3 = 0, úgy döntöttünk, hogy grafikusan öt módon. Elemezzük mi a lényege ezeknek a módszereknek.

I. módszer. Ábrázolva működését a metszéspontja az x tengelyen.

II módszer. Alakítsa át az egyenletet formájában ax 2 = -BH - építeni a parabola y = ax 2 és y = -BH -, hogy megtalálja a metszéspontja (gyökerei az egyenlet a abszcisszái metszéspontja, persze, ha van ilyen).

III folyamat. Egyenlet átalakítjuk a formájában ax 2 + c = - bx építmények parabola y - ax 2 + c, és a vonal az y = -BH (áthalad a származási); megtalálják a metszéspont.

IV módszer. Módszer alkalmazásával elosztása tökéletes négyzet alakítjuk formájában egyenlet

és (x + l) 2 + m = O
és további
és (x + I) = - m

Építsünk parabola y = a (x + I) 2, és az y = - m, párhuzamos az X tengellyel; megtalálják a metszéspont a parabola és egy egyenes vonal.

V módszer. Alakítsa át az egyenletet formájában

Építsünk hiperbola (e - hiperbola, feltéve, hogy) és az egyenes vonal az y = - ax - b; megtalálják a metszéspont.

Vegye figyelembe, hogy az első négy mód alkalmazható bármely egyenletek formájában ax 2 + bx + c = 0, egy öt - a csak azok, amelyekben p. A gyakorlatban, akkor választhat az is, hogy úgy gondolja, legalkalmasabb egy adott egyenlet, vagy hogy tetszik (vagy nem érti).

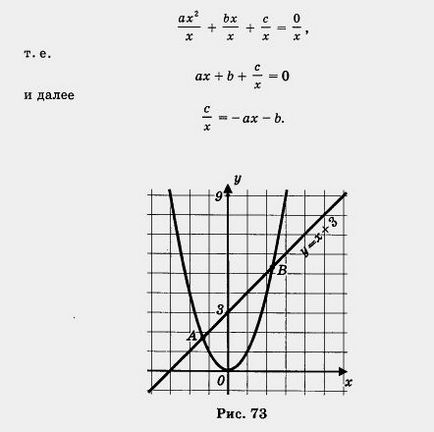
Megjegyzés. Annak ellenére, hogy számtalan módszer grafikai megoldások másodfokú egyenlet, bizalom a tényt, hogy a másodfokú egyenlet tudjuk oldani grafikusan, nem. Tegyük fel például, meg kell megoldani az egyenletet x 2 - x - 3 = 0 (külön figyelembe az egyenlet, amely hasonló ahhoz, amit a példák között tárgyaljuk). Próbálja azt, például, a második módszer: átalakítja az egyenlet x 2 = x 3 + konstrukció parabola y = 2, és
a y = x + 3, ezek metszéspontjai A és B (ábra. 73), majd az egyenletnek két gyöke. De mik azok a gyökerek, nem mondhatjuk, hogy a rajzot - az A és B pontja nem a „jó” helyzetben, mint a fenti példában. Most tekintsük az x 2-95 = 0. 16h- próbálja megoldani, például a harmadik módszert. Mi átalakítani az egyenlet a formában X 2 - 95 = 16x. Itt meg kell építeni a parabola y = X 2 - 95 és az y = 16x. De a korlátozott méretű lap notebook nem engedik meg azt, hogy nem, mert a parabola y = x 2 -ra kell csökkenteni 95 sejtek lefelé.

Így a grafikai megoldások a másodfokú egyenlet szép és kellemes, de nem ad teljes garanciát a megoldás bármely másodfokú egyenlet. Figyelembe vesszük azt, • egyéb.

Matematika letölthető. feladat hallgató 8 osztályú anyagok matematika Grade 8 interneten

Ha javításokat és javaslatokat a leckét, kérjük lépjen kapcsolatba velünk.

Ha azt szeretnénk, hogy a többi beállítást és javaslatokat órák, nézd meg itt - Oktatási fórum.