A legnagyobb és a legkisebb érték a függvény az intervallum

Tegyük fel, hogy a függvény az y = f (x) folytonos a [a, b]. Mint ismeretes, egy függvény az intervallumon eléri a maximális és minimális értékeket. Ezek jellemző értékek is eltarthat akár a belső pontját a [a, b], vagy határán a szegmens.

Megtalálja a maximális és minimális értékeket a függvény az [a, b] van szükség:

1) megtalálják a kritikus funkciót pont tartomány (A, B);

2) kiszámítja a függvény értékei találhatók a kritikus pontokat;

3) kiszámítjuk a függvény értékei a végpontokon, azaz az x = a és x = b;

4) az összes számított függvény értékei válassza ki a legnagyobb és a legkisebb.

Példa. Keresse meg a maximális és minimális értéke a függvény

Találunk a kritikus pontok:

Ezek a pontok esnek [0; 3]; y (1) = - 3; y (2) = - 4; y (0) = - 8; y (3) = 1;

azon a ponton, x = 3, és x = 0.

funkciók kutatása konvexitás és inflexiós pont.

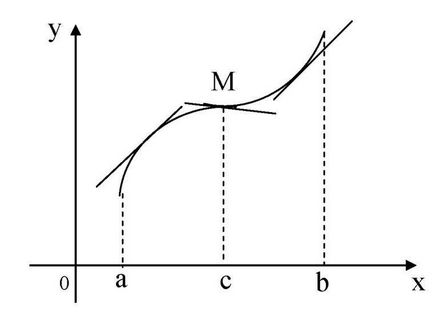
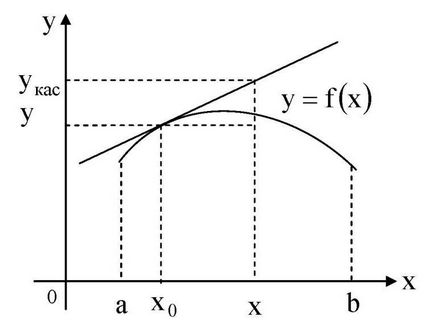
A függvény y = f (x) nevezzük vypukloyvverh az intervallum (a, b). ha annak grafikon alatt fekszik húzott érintő bármely pontján az intervallum, és az úgynevezett egy konvex lefelé (konkáv). ha grafikon felett fekszik az érintő.

A lényeg az átmenet, amelyen keresztül egy dudor van helyettesítve konkáv, vagy fordítva, az úgynevezett inflexiós pont.

Algoritmus kutatása konvexitás és inflexiós pont:

1. Naydemi kritikus pontok a második fajta, azaz azt a pontot, ahol a második derivált nullával egyenlő, vagy nem létezik.

2. Alkalmazza a kritikus pont a számegyenesen, osztja azt időközönként. Keresse meg a jele a második derivált minden intervallumban; Ha a függvény konkáv, ha a függvény konvex lefelé.

3. Amikor áthalad a kritikus pont a második fajta fog változni jel és ezen a ponton a második derivált nulla, ezen a ponton - az abszcissza az inflexiós pont. Megtalálja a koordináta.

Aszimptota a grafikon funkciók. A tanulmány a funkció az asymptote.

Definíció. Aszimptotájának a grafikon egy egyenes vonal. a tulajdonság, hogy a távolság bármely pontján a menetrend, hogy ezt a vonalat nullához eltávolításával pont a grafikonon az origó.

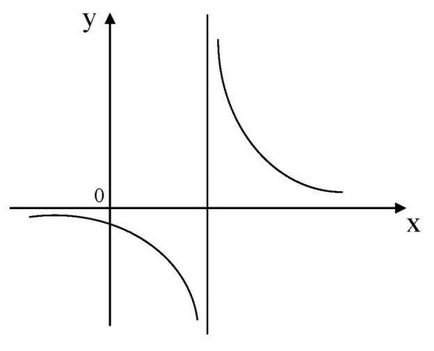
Három féle aszimptotákkal: függőleges, vízszintes és ferde.

Definíció. Közvetlen nazyvaetsyavertikalnoy aszimptotájának a grafikon y = f (x). ha legalább az egyik egyoldalú határértékek funkciót ezen a ponton megegyezik a végtelenig, hogy van,

ahol - a diszkontinuitás pontot, majd estne tartozik a domain.

X = 2 - töréspontot.

Definíció. Közvetlen y = A grafikon az úgynevezett vízszintes aszimptotájának a függvény y = f (x), ha