Személyes oldal - függvény szélsőérték
szélsőérték funkció
Extremum úgynevezett maximális vagy minimális érték függvény egy adott készlet.
szélsőérték pont - a pont, ahol a maximális vagy minimális függvény értéke.
A maximális pont - elér egy pontot, ahol a maximális érték a funkciót.
minimum pont - a pont, ahol a függvény értéke eléri a minimális értéket.
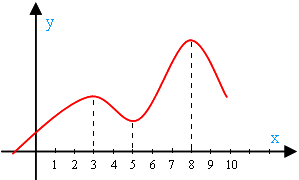
Az ábra a közelben X = 3, a függvény eléri a maximális értéket (azaz, a közelben e pont nem az a lényeg a fenti). A környéken x = 8 újra, hogy van egy maximális érték (ismét egyértelmű: ez az a környéken nincs pont fölött). Ezeken a pontokon, a növekedés csökkenését váltotta. Ezek a pontok maximum:
A szomszédságában X = 5 elérte a minimális értéket a függvény (azaz, a közelben a X = 5 pont alatti No). Ezen a ponton, a csökkenés helyett növekedés. Ez egy minimum:
Pont a legnagyobb és legkisebb pont extrém funkciókat. és a függvény értékei ezeken a pontokon - a szélsőségek.
Ho pont a maximális pontot. ha van egy olyan környéken, minden ponton, ahol f (x) kisebb vagy egyenlő, mint f (Ho):
Egyszerűsített megfogalmazás. ha Ho-származék előjelet származó plusz mínusz, akkor Ho a maximális pontot.
ho van egy pont minimum. ha van egy olyan környéken, minden ponton, ahol f (x) nagyobb vagy egyenlő, mint f (Ho):
Egyszerűsített megfogalmazás. ha Ho-származék előjelet mínusz plusz, akkor Ho egy minimális pontot.
Kritikus és stacionárius pont a függvény:
Belső pontja határozza meg a funkciót, amelyben a függvény folytonos, de a származékos nem létezik, az úgynevezett kritikus pont.
Belső pont domain a funkció, amely a derivált nulla, az úgynevezett fix pont.
Ennek szükséges feltétele extrémuma:
Ha Ho - pont szélsőérték az f (x), akkor ezen a ponton vagy származékát Vanishes (ezt a stacionárius pont) vagy származékát nem létezik (a kritikus pont).
Elégséges feltétele szélsőérték:
Let Ho - a kritikus pont. Ha a származék f „(x) való átmenetnél balról jobbra a ponton át Ho változik jele a plusz mínusz, a Ho - maximális pont:
Ha a származék f „(x) való átmenetnél balról jobbra a ponton át Ho változik jele mínusz plusz, a Ho - a minimális pont:
Ha átmegy a kritikus pont a származék nem változik jel, akkor azon a ponton, Ho nincs szélsőérték.
Az [a, b] az y = f (x) elérheti a legkisebb vagy a legnagyobb értéket, vagy a kritikus pontokat vagy szegmensek végein [a, b].
2) Find rögzített (f '(x) = 0), és a kritikus (f' (x) nem létezik) a pont funkció y = f (x).
3) Jelölje a helyhez kötött és a kritikus pontok száma sorban, és határozza meg a megjelölés a származék a keletkező hézagokat.
4) következtetéseket levonni a monotónia a funkció és a pontok szélsőérték.