Solutions egyenletek (megtalálni a gyökerei az egyenlet), a tartalom platform
Solutions egyenletek (megtalálni a gyökerei az egyenlet)
Egyenlet - az egyenlőség két kifejezést változókkal.
Oldja meg az egyenletet -Find gyökerei az egyenlet vagy annak bizonyítására, hogy nem azok.
1. Bontsa ki a zárójelben esetleges alkalmazása forgalmazás és ingatlan
egy (b + c) = a b + a C
(A + b) (c + d) = a C + D + b c + b d
2. A gyökerei az egyenlet nem fog változni, ha van ilyen - a kifejezés át az egyik része az egyenletnek egy másik, változó jel.
(Mondván változót gyűjteni, hogy egyik oldalán a másik oldalon, és a változó a jelek szempontjából a számok, amikor áthalad a egyenlőségjel.) Példa:
3 (2 + 1,5 x) = 0,5 x + 24
6 + 4,5 x = 0,5 x + 24
4,5 X - = 0,5 x 24-6
Példa: kiszámítja koordinátái metszéspontok a sor 5 x 7 + y = 105 a koordinátatengelyek.
Megoldás: 1), hogy az x-tengelyen (21, 0)
y = 0; X 5 + 7 * 0 = 105 így x = 21
2) a tengellyel OY pont (0; 15)
X = 0; 5 * 0 + 7 = 105 van itt y = 15
A: az X-tengelyen (21, 0) és a DU tengelye pont (0; 15).
3. A gyökerei az egyenlet nem változik, ha a két rész az egyenlet szaporodnak vagy
osztva az azonos számú nem egyenlő 0-
A termék értéke 0. Ha az egyik
0. tényezők, megoldjuk a másodfokú egyenlet:
= 0 Tétel Wyeth van
Def. Megoldása az egyenletrendszert kétváltozós egy pár a változók értékeit megközelíthető minden egyenletét a rendszer valódi egyenlőséget.
Megoldási módjait, egyenletrendszerek.
1) grafika (grafikus össze egy egyenletrendszer, megkapjuk a grafikonok metszéspont koordinátáit metszéspontok lesz oldatok egyenletek).
építeni különálló vonalak 2 grafikus + 3y = 5 és 3y = - 9
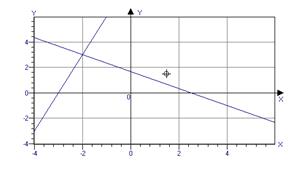
Építünk grafikonok ezeket a funkciókat egyetlen koordinátarendszerben, és megtalálja a koordinátáit metszéspontok. Ebben a példában, egy keresztezési pont és annak koordinátái x = - 2 és y = 3.
2) helyettesítő módszer (expressz egy változót át egy másik a helyettesítő egyenlet a második egyenlet megoldására a kapott egyenletet egyetlen változó, a talált érték helyettesítő változót a második egyenletben, és megtalálja a második változó. És írni válasz)
Példa. oldja meg a rendszer egyenletek
- 5x +2 (7 - 3x) = + 4Y) - 2y = 30
-5x +14 - 6x = 3 75 + 12y - 2y = 30
-11x = 3-14 10y = 30-75
- 11x = - 11 10y = - 25
X = 1, y = 7 - 3 = 4 * 1 y = - 2,5 x = 25 + 4 * (- 2,5) = 15
Válasz. x = 1; y = 4 Válasz: x = 15; y = - 2,5
3) addíciós módszer (szaporodnak mindkét oldalán az első egyenletben, hogy egyetlen szám. Mindkét fél a többi egyenlet egy másik számra, a két szám olyan, hogy azok a szorzatát azonos változók ellentétes együtthatók)
Példa. oldja meg a rendszer egyenletek
A: a = 10 b = 5
Példa: oldja az egyenletrendszert
Válasz: X = - 10, y = 5
Példa: kiszámítására koordinátáit metszéspontok sor
2 x - 3 és y = 7 + 5 x 4 y = 6
Határozat: a feltétel a pontok koordinátáinak kielégítik mindkét egyenlet, akkor van megoldás az egyenletek a rendszer.
Közvetlen y = k x + b áthalad a pont (- 1, 3) és B (2; Írja egyenletét ezen a vonalon.
Megoldás: közvetlen helyettesítő egyenlet koordináta értékeket adott pontot, és megszerezni a rendszer egyenletek.
Példa: oldja az egyenletrendszert
Következő megoldjuk kívül módszer
Helyettesítsük be az első egyenlet
Find koordinátáit metszéspontok (-2, -1). (-2, 1). (2, -1). (2: 1)
Ezért azt megoldására két egyenletrendszerek.
Megoldása az adagolási módszert get: