Solid deformáció - studopediya

Figyelembe véve, hogy a merev test mechanika, szoktuk a koncepció egy merev test. Azonban a természetben nincs merev testek, hiszen minden igazi test erői változik alakja és mérete, azaz a. E. deformálódott.

Deformáció nazyvaetsyauprugoy ha a szervezet megkapja az eredeti méreteit és formu.Deformatsii hogy fennállnak a szervezet megszűnése után a külső erők, nazyvayutsyaplasticheskimi (iliostatochnymi) megszűnését követően a külső erők. Teste az intézkedés alapján a külső erők, inkább a tapasztalat rugalmas és képlékeny alakváltozás a műanyag, mivel ezek megszűnése után a külső erők soha nem fog teljesen eltűnni. Azonban, ha a maradék deformációk kicsik, lehet figyelmen kívül hagyni, és úgy csak rugalmas alakváltozás, ami mit fogunk csinálni.

A rugalmasság bebizonyította, hogy mindenféle törzs (feszültség vagy nyomás, nyírás, hajlítás, csavarás) lehet csökkenteni, hogy a deformáció egyszerre előforduló nyújtás vagy tömörítés és nyírás.

Tekintsünk egy homogén rúd L hosszúságú, és a keresztmetszeti területe S (ábra. 34), amelyhez kapcsolódnak végein erőt irányított a tengelye mentén. miáltal a rúd hossza változik nagyságát. Természetesen, amikor a feszültség pozitív és nyomó - negatívan.

A ható erő egységnyi keresztmetszeti területe, nazyvaetsyanapryazheniem:

Ha az erő mentén irányul normális a felületi feszültség nazyvaetsyanormalnym, ha egy érintőleges a felszínre -tangentsialnym.

A kvantitatív mértékét deformáció, a próbatest egootnositelnaya deformáció. Így, a relatív változás a rúd hosszát (hosszanti törzs)

relatív kereszt feszültség (tömörítés)

ahol a d - rúd átmérője.

Deformáció, és mindig van különböző jelek. A tapasztalat a kapcsolatuk a következő:

ahol - pozitív együtthatójú függően anyagtulajdonságok, Poisson nazyvaemyykoeffitsientom (S. Poisson (1781-1840) - francia tudós).

Angol fizikus Robert Hooke (1635- 1703) a kísérleti megfigyelésekkel, hogy a kis törzsek, nyúlás és feszültség egyenesen arányos egymással:

ahol az arányossági tényező az úgynevezett Young-féle modulussal E (Young T. (1773-1829) - brit tudós).

Tól (21,3) látjuk Jung chtomodul által meghatározott feszültség, ami nyúlása egy. A képletek (21,2), (21.3) és (21.1), amely

ahol k a rugalmassági tényező. Egyenlet (21,4) is állítja a Hooke-törvény, amely szerint a kiterjesztés rúd rugalmas alakváltozás arányos erő hat a rúd.

Deformációja szilárd engedelmeskedik Hooke-törvény csak nagyon szűk határok (erejéig arányosság). A további növekedés a feszültségfüggése már nem lineáris, bár a rugalmas alakváltozás rugalmas, amíg meg előre () és a maradék deformációk nem fordul elő. Rugalmassági határán túl a szervezetben, amelynek a maradék törzsnél, vagyis test eredeti állapotába megszűnése után ébredő erő nem kerül vissza. A feszültség, amelynél érzékelhető maradék törzs ( „0,2%) nazyvaetsyapredelom kitermeléssel (). A deformáció növekedésével nélkül feszültség növelésével, azaz a. E. Body, mint a „folyó”. Ez a terület hozam nazyvaetsyaoblastyu (ilioblastyu képlékeny alakváltozás). Olyan anyagok, amelyek az áramlási területe jelentős, nazyvayutsyavyazkimi, és amelyre az áramlási gyakorlatilag otsutstvuet- törékeny. A további megnyúlását a test a pusztulástól. A maximális feszültség a szervezetben termelődő, hogy törési szilárdsága nazyvaetsyapredelom ().

Ugyanez merev test által rövid akció erők megmutatkoznak a törékeny és hosszú, de gyenge teljesítmény áramlik.

Uprugorastyanutogo számítani a potenciális energia (tömörített), amely a rúd egyenlő a munkát a külső erők deformáció során:

ahol x - abszolút hosszabbító rúd, amely közben változik deformációja 0do. Szerint a Hooke-törvény (21,4). ezért

t. e. uprugorastyanutogo potenciális energiája deformáció négyzetével arányos rúd.

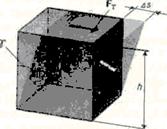
Nyíró deformációt a legkönnyebb végrehajtani, ha take bar alakú egy négyszögletes parallelepipedon alakú, és ehhez csatlakozik az erő (Fig.36), az érintő a felületére (alsó része a sáv fixen van rögzítve). Relatív nyíró deformációt határozzuk meg a képlet

ahol - az abszolút elmozdulása párhuzamos rétegek a test egymáshoz képest; H - a távolság a rétegek (kis szögek).

· Mi az tehetetlenségi nyomatéka a test?

· Mi a szerepe a tehetetlenségi nyomaték a rotációs mozgás? Mi az a képlet mozgási energia egy test körül forgó egy rögzített tengely, és hogyan lehet ez?

· Mi a neve a pillanatban egy erő egy rögzített pont körül? viszonyítva rögzített tengely? Milyen az irányt a pillanatban az erő?

· Kijelző és adja meg a dinamikai egyenlet a forgómozgást szilárd. Mi a perdület egy anyagi pont? Solid State? Milyen az irányt a perdület?

· Mi az a fizikai természet törvényének megőrzése perdület? Egyes rendszerekben fut? Adjon példát.

· Milyen szimmetria tulajdonságainak tér határozza meg az érvényességét a törvény megőrzése perdület?

· Mi a szabad tengely (főtengelye tehetetlenség)? Melyik ezek közül a stabil? Mi a giroszkóp? Mik a főbb jellemzői?

· Fogalmazza Hooke-törvény. Amikor tisztességes?

· Mennyi az arányosság, a rugalmasság és az erő? Mi a fizikai értelmében a Young-modulus?

4.1. Az egyik szint a ferde síkok egyidejűleg kezd csúszásmentesen gördülni tömör henger, és egy gömb, amely azonos tömegű és azonos sugárral. Adjuk meg: 1) az aránya a sebessége a henger és egy gömb az adott szinten; 2) aránya egy adott időben. [1) 14/15; 2) 14/15]

4.2. A homogén szilárd lemez pereme sugara R = 0,5 m alkalmazott állandó tangenciális erő F = 100 N. Amikor a lemez forog, hogy hat a súrlódási nyomaték M H = 2 m. Határozzuk meg a M tömegét a lemezt, ha ismeretes, hogy a szögletes gyorsulás állandó és egyenlő 12 rad / s 2 [32 kg]

4.3. Miután rögzítő egység formájában tömör henger teszi egy homogén massza m = 1 kg akasztott súlytalan menet, amelynek végei kapcsolódnak be a testtömeg 1 kg = 2 kg. Elhanyagolása súrlódás a blokk tengely meghatározására: 1) a gyorsulás az árut; 2) a kapcsolat szálfeszítő erők. [1) 2,8 m / s 2; 2) 1,11]

4.4. Kerék forgási sebesség, amely tehetetlenségi nyomaték m 2 kg 2. ravnozamedlenno forgó fékezéskor, az idő t = 1 perc-re csökkent 300 / perc 180 ford / perc. Adjuk meg: 1) a szöggyorsulás a kerék; 2) A fékerő M nyomatékot; 3) A munka a fékerő. [1) 0,21 rad / s 2; 2) H 0,42 m; 3) 630 J]

4.5. Egyedi tömeg m = 80 kg, állt a szélén egy vízszintes platform tömeg M = 100 kg forgó által tehetetlenségi rögzített függőleges tengely frekvenciája 10 / perc, bevételt a központ. Feltételezve, hogy egy egységes platform kerek, tárcsa, hanem egy ember - egy pont tömeget, hogy meghatározzuk a gyakoriság, amellyel ekkor elfordul a platform. [26 ford / min]

4.6. Határozzuk meg a alumínium rúd nyúlása feszültség alatt fordított munkamennyiség 621 J. szár hosszát 2 m, a keresztmetszeti területe 1 mm 2 Young-modulusza alumínium E = 69 GPa. []