Minden képlet matematika

előző ◈ a következő

Ez az oldal tartalmazza az összes képlet szükséges a vizsgálaton, és önálló művek, vizsgák algebra, geometria, trigonometria, szilárd geometria és egyéb ágak matematika.

Itt lehet letölteni vagy néz online az összes alapvető trigonometrikus képlet, a képlet terület a kör, a képletét rövidített szorzás formula kerületű csökkentési képlet és még sokan mások.

Azt is ki kell nyomtatni a szükséges gyűjtemények matematikai képleteket.

Academic siker!

Arithmetic Formula:

Algebra képlet:

Geometriai képlet:

Matematikai képlethez:

Törvények műveletek számát

Kommutatív joga továbbá: a + b = b + a.

Az asszociatív törvény mellett: (a + b) + c = a + (b + c).

Kommutatív törvénye szorzás: ab = ba.

Az asszociatív törvény szorzás: (ab) a = a (bc).

Elosztó törvénye szorzás feletti mellett: (a + b) c = AC + bc.

Elosztó törvénye szorzás tekintetében kivonás: (a - b) c = AC - bc.

Néhány matematikai szimbólumok és rövidítések:

Minden képlet matematika

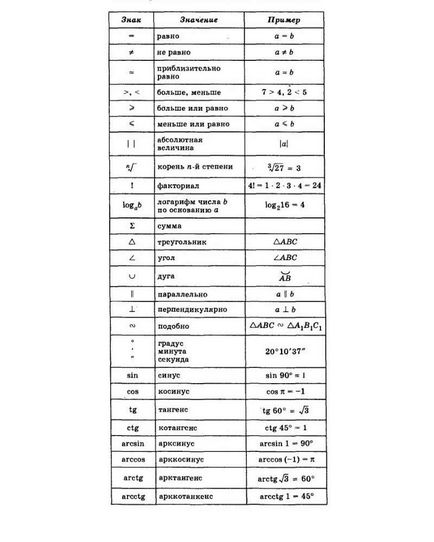
jeleit oszthatóság

Jelei oszthatóság „2”

Osztható számot „2” nyom nélkül nevezik még. nem osztható - páratlan. A szám osztva „2” maradék nélkül, ha az utolsó számjegy chotnaya (2, 4, 6, 8) vagy nulla

Jelei oszthatóság „4”

A szám osztva a „4” nyom nélkül, ha az utolsó két számjegye az O vagy X összeget képez osztható számot „4”

Jelei oszthatóság „8”

A szám osztva a „8” nyom nélkül, ha az utolsó három jegyeinek nulla vagy az összeg képezi a számok osztható „8” (például: 1000 - az utolsó három számjegy „00”, és elosztjuk 1000 8 fordul 125 104 - az utolsó két „12” vannak osztva négy számjegy, és elosztjuk a kapott 112 4 28; stb)

Jelei oszthatóság „3” és „9”

Anélkül, hogy a mérleg a „3” vannak osztva csak azok számok, melyek összege a számjegyek osztható „3”; A „9” - csak azokat, amelyek összege számjegy osztható „9”

Jelei oszthatóság „5”

Anélkül, hogy a mérleg a „5” vannak osztva a szám az utolsó számjegy „0” vagy „5”

Jelei oszthatóság „25”

Nem maradékot „25” vannak osztva száma, utolsó két számjegye, amelyek nulla vagy az összeget képeznek számokat osztható „25” (vagyis azt a számot végződő „00”, „25”, „50”, „75 "

Jelei oszthatóság „10”, „100” és „1000” A

Anélkül, hogy a mérleg a „10” vannak osztva csak a számot, az utolsó számjegy a nulla, a „100” - csak azokat a számokat, amelyek az utolsó két számjegye nulla a „1000” - csak azokat a számokat, amelyek az utolsó három számjegye nulla

Jelei oszthatóság „11”

Anélkül, hogy a mérleg a „11” vannak osztva csak azok számok, melyek összege a számjegyek, elfoglal furcsa helyeken, vagy egyenlő a számok összege, amelyek elfoglalják a még helyek, vagy eltér ez a szám osztható „11”

Az abszolút értéke - általános képletű (modul)

Formula végzett műveletek A frakciók

Egy inverziós formula a végső decimális racionális frakció:

Két egyenlő kapcsolatok képezik aránya:

A fő tulajdonsága aránya

Megtalálni a tagok aránya

Arányokat. egyenértékűek arányok. Származtatott aránya - következésképpen adott hányadát

Az átlagértékeket

számtani átlaga

Geometriai átlag (középérték arányos)

négyzetes középértéke

harmonikus középérték

Néhány véges sorozat

Azonos átalakítások algebrai és trigonometrikus kifejezések

tulajdonságai hatáskörök
  • Minden x, y, és a és b pozitív valódi egyenlőség:

  • Tulajdonságok számtani gyökerek

    Tetszőleges pozitív egész n, és a K, 1-nél nagyobb, és bármely nem negatív a és B igaz egyenlőséget:

  • polinomok

    • Minden a, b, c igaz egyenlőséget:

    Tulajdonságai numerikus egyenlőtlenségek

    1) Ha a

    5) Amennyiben a

    7) Ha egy 0. b> 0. Ekkor

    Közötti kapcsolatok trigonometrikus függvények azonos érv

    (A továbbiakban a felvétel n Je Z azt jelenti, hogy az n - bármilyen egész szám)

  • Ezenkívül képletek:

    Formula kettős érv:

    Formula hármas érv:

    Képlet fele az érv:

    (A funkciók sin és cos - a mértékét csökkentő általános képletű)

    Formula harmadik és negyedik fokozat:

    Formula összegek átalakítása egy termék:

    Formula konverziós termék mennyiségét:

    képlet a átalakítására kifejezések az űrlap a) hogy az adott funkciót megjelölés, amely az eredeti funkció; b) a funkció megváltozott „kofunktsiyu”, ha n páratlan; funkció nem változik, ha n páros. (Kofunktsiyami szinusz, koszinusz, tangens és kotangens hívnak koszinusz, szinusz, és érintőleges kotangensét.) Például:

    Formula megállapítás szög:

    Értéktáblázat

    Az egység kör:

    A képlet a haladás:

    számtani sor

    (A1 - az első tag; d - különbség; n - a tagok száma; egy - n-edik tagja; Sn - összege az első n):

    mértani sorozat

    (B1 - az első tag, q - a nevező n - a tagok száma; Mrd - n-edik ciklus; Sn - összege az első n tagok, S - összege végtelen progresszió Geom.):

    derivált

    Az alapvető szabályok differenciálás:

    A származék egy összetett függvény:

    Ha az f függvény egy származékát egy ponton XO, és a g függvényt egy származékával yo = f (XO), a komplex függvény h (x) = g (f (x)) is egy származékával XO, ahol:

    Származékai trigonometrikus függvények:

    A származék a logaritmikus függvény:

    Az egyenlet az érintő a függvény grafikonját:

  • A mechanikus értelmében származék:
  • 1) v (t) = x „(t);
  • 2) a = V „(t).
  • Geometriai értelmében a származék:
  • logaritmusok:
    Minden képlet matematika
  • Koordináták és vektorok

    1. A pontok közötti távolság az A1 (x1, y1) és A2 (x2; y2) képlet adja meg:

    2. A koordináták (x; y) a középpontját a végek A1 (x1, y1) és A2 (x2; y2) által tárolt képlet:

    3. A vonal egyenlete egy lejtőt és a metszetet a formája:

    Szög K együttható értéke a szög tangense által alkotott egyenes vonal és a pozitív iránya Ox tengely és a metszetet q - értéke az ordináta a metszéspont az egyenes a tengellyel Oy.

    4. Az általános egyenlete egyenes vonal a formában: ax + by + c = 0.

    5. egyenletek egyenes vonalak párhuzamosak, illetve tengelyek Oy és Ox, az alábbi formájú:

    6. feltételek párhuzamos és merőleges vonalak y1 = kx1 + Q1 és y2 = kx2 + q2, illetve, az alábbi formájú:

    7. A kör egyenlete R sugarú, és O középpontú, illetve a pontok (0, 0) és a C (XO; yo) van formájában:

    Ez jelenti egy egyenlet egy parabola a vertex a ponton abszcisszájú

  • Descartes-féle derékszögű koordináta-rendszer az űrben

    1. A pontok közötti távolság az A1 (x1; Y1; Z1) és A2 (x2; Y2; Z2) képlet adja meg:

    2. A koordináták (x; y; z) a végei a középső szegmens A1 (x1; Y1; Z1) és A2 (x2; Y2; Z2) az alábbi:

    3. modul vektor által meghatározott koordinátái adják:

    4. hozzáadásakor vektorokat a megfelelő koordináták vannak kialakítva, és megszorozzuk a vektor számos összes koordinátáit szorozni ezt a számot, azaz következő képletek:

    5. Az egység vektor codirectional a vektorral a következő képlet szerint:

    6. A skalár termék száma:

    ahol - közötti szög a vektorok.

    7. A dot termék két vektor

    8. A koszinusza közötti szög vektorok és adja meg:

    9. A szükséges és elégséges feltétele merőleges vektorok és a formája:

    10. Az általános egyenlete merőleges síkban a vektor a formája:

    ax + by + cz + d = 0.

    11. A egyenlete merőleges síkban a vektor és ponton áthaladó (xo; yo, zo), a formája:

    egy (X - XO) + b (y - yo) + c (z - zo) = 0.

    12. Az egyenlet a gömb középpontja O (0, 0, 0) van írva, mint:

    1) A bizonyos permutációi n elem adja meg:

    2) A szabályozások számát elemek n m általános képletű:

    3) A kombinációk száma n elemeinek m adja meg:

    4) A következő kombinációját tulajdonságok:

    5) általános képletű binomiális a formája:

    A számok összege a és b értéke n.

    6) (k + 1) -edik kifejezés adja meg:

    7) A kombinációk száma is megtalálható a háromszög Pascal.

    Pascal háromszög (legfeljebb n = 7):

    8) összege binomiális együtthatók egyenlő, mint 2n.

    9) Ahhoz, hogy megtalálja a következő tagja a binomiális együttható, szükséges binomiális együttható szorozva az előző tag egy alak, és osszuk el a számos korábbi tagjai.

    Ez az a kör közepén - a metszéspont midperpendiculars. Központja a beírt kör - a metszéspontja a szögfelező. (A, B, C - oldalán - szemközti szögek rájuk; p - semiperimeter; R - sugara a körülírt kör; r - a sugara a beírt kör; S - terület; ha - magassága hívni az oldalán egy):

    2. Egy derékszögű háromszög:

    A központ a körülírt kör egybeesik a központja a átfogója. (A, b - a lábak, c - átfogója; ac, bc - vetülete a lábak a átfogója):

    3. Az egyenlő oldalú háromszögben:

    Medián felezővonal. = Vagy.

    4. Egy tetszőleges konvex négyszög

    (D1 és D2 - átlós - szög kiképezve; S - terület):

    (A és B - szomszédos oldala, - a köztük lévő szög; ha - magassága hívni az oldalán egy):

    Mindenesetre gyémánt kör írható,.

    Akkor le egy kört minden téglalap.

    (A és B - egy bázis, H - távolság van kiképezve; l - középső sor):

    10. Meghatározza sokszög

    (P - semiperimeter; R - a sugara a beírt kör):

    S = pr. 11. A szabályos sokszög

    (An - jobb oldali n-szög; R - sugara a körülírt kör; r - a sugara a beírt kör):

    (R - sugara; C - kerülete; S - területe egy kör):

    (L - ívhossz határoló ágazatban - fokú intézkedés a központi szög, - a radiánban központi szög):

    • Stereometriya1. önkényes prizma

      (L - oldaléle; P - az alap kerületét; S - lábnyom, H - magassága; Psech - merőleges a keresztmetszet kerülete; Sbok - palástfelületén; V - v):

      2. Közvetlen prizma 3. kocka alakú

      (A, B, C - méretei; V - átlós):

      5. Tetszőleges piramis

      (S - lábnyom, H - magassága; V - v):

      6. Helyes piramis

      (P - az alap kerületét; l - apothem; Sbok - palástfelületén):

      7. tetszőleges csonka gúla

      (S1 és S1 - négyzet bázisok; H - magassága; V - v):

      8. Helyes csonka gúla

      (P1 és P2 - kerülete bázisok; l - apothem; Sbok - palástfelületén):

      (R - sugara a bázis, H - magassága; Sbok - palástfelületén; V - v):

      (R - sugara a bázis, H - magassága; L - generátor; Sbok - palástfelületén; V - v):

      (R - a gömb sugara; S - területe a gömb alakú felület, V - v):

      (R - a gömb sugara; H - magassága szegmens; S - gömbszelet felületű; V - v):

      (R - a gömb sugara; H - magassága szegmens; V - v):

    előző ◈ a következő