meghatározása a származékos

Ez a cikk ad alapfogalmak, amely alapján minden további elmélet származék függvényében egy változó.

Path x - az érvelés f (x), és - egy kis számú nem nulla.

(Olvassa el a „Delta X”) nevezik a növekmény az érvelés. Az ábrán a piros vonal mutatja a változást érv az x értékének az értéket (itt látható a nevei „növekményt” érv).

Ha a berendezéssel az értéke az érv a függvény értéke rendre változhat alanyról monotonitás a szegmens. A különbség az úgynevezett egy növekménye f (x). ennek megfelelő növekmény az érvelés. Az ábrán a növekmény funkciót kék vonal.

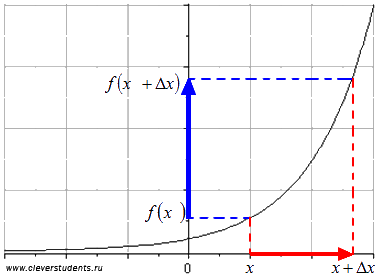
Vegyük ezeket a fogalmakat egy konkrét példát.

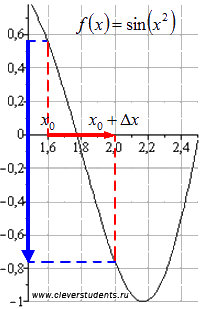
Vegyük például a funkciót. Fix pont és a növekmény az érvelés. Ebben az esetben, a növekmény a funkció az átmenetet a még meg kell

Csökkenti mondta a bomlási funkció az intervallumon.

Meghatározása származéka egy függvény egy ponton.

Tegyük fel, hogy az f (x) meghatározott intervallumban (a; b). és - a pont ebben az időszakban. Deriváltja az f (x) egy pontban úgynevezett határa az arány a növekmény, hogy a növekmény funkciót érv. Jelezték.

Mikor volt az utolsó korlát veszi sajátos véges értéket, majd beszélni, hogy létezik egy véges származék egy ponton. Ha a határ végtelen, akkor azt mondjuk, hogy a származék végtelen ezen a ponton. Ha a határérték nem létezik, akkor a függvény deriváltját ezen a ponton nem létezik.

f (x) függvény differenciálható azon a ponton, ha van egy véges-származék ott.

Ha az f (x) differenciálható minden pontján az intervallum (a; b). A funkció az úgynevezett differenciálható ezen az intervallumon. Így, bármely pontja x intervallumban (a; b) társítható a értéke differenciálhányados ezen a ponton, hogy van, képesek vagyunk meghatározni egy új funkciót, amely az úgynevezett függvény deriváltját f (x) az intervallum (a; b).

A művelet a megállapítás a származékos hívják differenciálás.

Döntetlen különbséget a természet a fogalmak differenciálhányados egy pont és egy intervallum: a függvény deriváltját ponton - ez a szám, és a függvény deriváltját intervallumban - ez a funkció.

Keresse meg a származék egy függvény egy ponton, a meghatározás.

Mivel keresünk egy függvény deriváltját az intervallumot, akkor a válasz kell fordulni funkciót. Vegyük ahol x - bármely számot az intervallumban. Definíció szerint, a származék egy határ, hogy az arány a növekmény funkciója a növekmény az érvelés, a növekmény az érvelés nullához:

Így jött a bizonytalanság. Ahhoz, hogy megtalálja ezeket a korlátokat a szorzás a konjugátum kifejezés utána alkalmazásával képletek Rövidítés megszorozzuk működtetése az ilyen kifejezések és rövidítések:

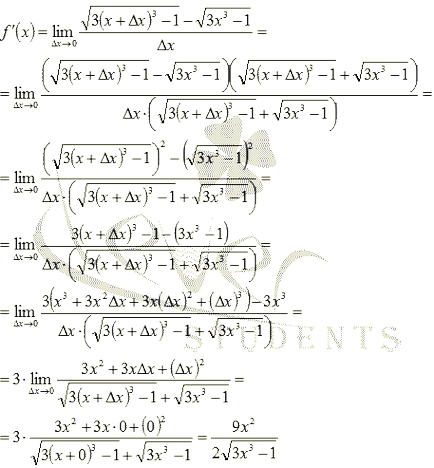
Nézzük összpontosít egy nagyon fontos pont: a domain az f (x) nem mindig esik egybe a domain a származék. Megjegyezzük, hogy az előző példában, a domain a funkció a kezdeti intervallumban, és a származék meghatározott intervallumban. Mit akarunk mondani. Tehát, hogy ha különbséget az ideális válasz: ez a funkció egy származéka az f (x) intervallumban

Ennek alapján a meghatározása képlet származéka kapott sok asztal származó alapvető elemi függvények, amelyek nagyon felgyorsítja differenciálás. A koncepció a származék is használják a bizonyíték a levezetési szabályok.