Kiszámítása területek síkidomok segítségével integrálok
Ebben a leckében megtanuljuk területének kiszámítására síkidomok. amelyek által határolt az abszcissza tengely (Ox), egyenes vonalú szegmenseket x = a. X = b, és az ütemezés a folyamatos és nem-negatív függvény y = f (x) értékek esetén „X”, az [a. b]. Ez a szám az úgynevezett görbe vonalú trapéz. Oldalsó szegmensek degenerálódhat hogy egy pontot. S ilyen méretű görbe vonalú trapéz lehet kiszámítani a következő képlet segítségével
Így a határozott integrál egy nemnegatív folytonos függvény f (x) az [a. b] (függvény grafikon felett található tengely Ox) számszerűen egyenlő a területet a görbe trapéz egy bázissal [a. b]. grafikon korlátos fenti függvény az y = f (x). Ez a geometriai jelentése a határozott integrál. Rajzok a számok - a példákban.
Ha f (x) ≤ 0 (függvény grafikon alatt található a tengely Ox), a terület a görbe trapéz lehet kiszámítani a következő képlet segítségével
Még mindig vannak olyan esetek, ahol mind a felső és alsó határát a szám - funkciót, illetve y = f (x) és y = φ (x). A terület az ábra képlettel számítottuk ki
Így a számítás a területek síkidomok - az egyik legfontosabb alkalmazások, amelyekben a határozott integrál a legtermékenyebb alkalmazást. Minden általunk vizsgált adatok elemi geometria, amely lehetővé teszi, hogy területének kiszámítására egyenes vonalú formák - téglalap, háromszög és sokszögek. Ami a hajlított formák, van megtalálásához területének segítségével az elemi geometria már nem elég. Tehát az üzletet. Megtanulják, hogyan kell alkalmazni, amit meghatározott a tetején ezt a cikket.
Kezdjük azzal az esettel, ahol az adott terület a szám lehet képlettel számítjuk ki (1).
1. példa Find területe az ábra által határolt ütemezés funkció, az abszcisszán (Ox) tengely és az egyenes vonalak az x = 1, X = 3.
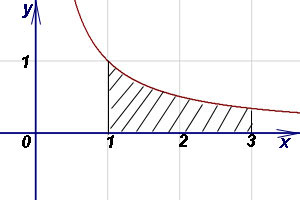
Határozat. Mivel y = 1 / x> 0, az [1; 3]. a területet a görbe vonalú trapéz következő képlettel (1):
2. példa Find a terület az ábrán korlátos függvény grafikon vonal az x = 1, és az abszcissza tengely (Ox).
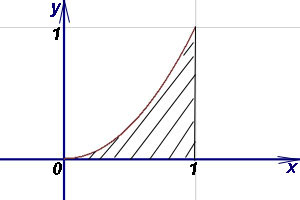
Határozat. A képlet szerint (1), van
Ha az S = 1/2; ha, hogy s = 1/3. stb
3. példa Find a terület az ábra által határolt ütemezés funkció, az abszcissza tengely (Ox) és egy egyenes vonal x = 4.
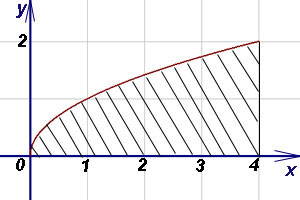
Határozat. Keresek ábra - görbe vonalú trapéz, amely elhagyta szegmens degenerálódott, hogy a pont. Integrációs határok 0 és 4. Mivel képlet szerint (1) található a terület a görbe vonalú trapéz:
Példa 4. Keresse meg a területet az ábra vonallal körülhatárolt található és az 1. negyedben.
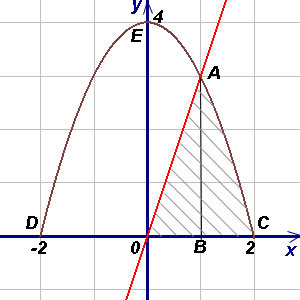
Határozat. Ahhoz, hogy a általános képletű (1) képviseli a területen a kívánt alakú formában a területének összege háromszögek OAB-hez és görbe vonalú trapéz ABC. Kiszámításakor az háromszög területe OAB integrációs határértékek a abszcisszán pontok O és A. számadatok és az ABC - abszcisszán az A és C pontok (A jelentése a metszéspont a parabola és az egyenes vonal OA, és C - a metszéspont a parabola tengelyével Ox). Megoldása (mint rendszer) egy egyenes vonal, és egy parabola, megkapjuk (abszcissza A pont) és (abszcissza a másik metszéspontja egy egyenes vonal, és egy parabola, amely nem szükséges a határozat). Hasonlóképpen, azt kapjuk, (abszcissza C és D pontok). Így már mindent, hogy megtalálják a terület az ábra. találunk:
Példa 5. Keresse meg a területet a görbe vonalú trapéz ACDB. Ha az egyenlet a görbe CD és abszcissza az A és B, illetve az 1. és 2..
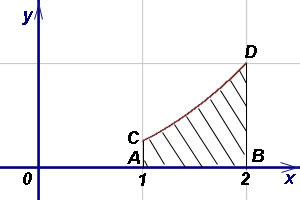
Határozat. Express keresztül az egyenlet a görbe y: Terület görbe vonalú trapéz következő képlettel (1):
Azt viszont, hogy az esetben, ha a terület a szám lehet kiszámítani képletű (2).
6. példa Find a terület az ábra által határolt parabola és az abszcissza tengely (Ox).
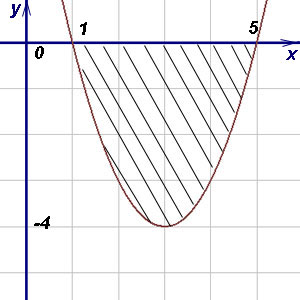
Határozat. Ez a szám alatt található az X tengely. Ezért ahhoz, hogy kiszámítsa a felhasználási terület (2). A határértékek az integráció az abszcissza és metszéspontjai a parabola tengelyével Ox. ezért
7. példa Find terület, bezárt az abszcissza tengely (Ox) és a két szomszédos szinusz hullámok.
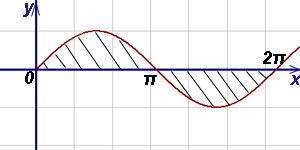
Határozat. A terület a szám lehet a következő képlettel (2):
Engedje meg, minden távon:
Végül találunk a környéken:
8. példa Keresse meg a területet a szám, és arra a következtetésre jutott a parabola görbe.
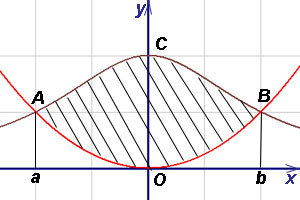
Határozat. Fejezzük sor egyenletet y:
Alatti területet (2) képletű, hogyan lehet megszerezni
ahol a és b - abszcissza az A és B pontok megtaláljuk őket, egyenletek megoldására:
Végül találunk a környéken:
Végül, az esetek, ahol a terület a szám lehet számítani a (3) képlet.
9. példa Find a terület az ábra által határolt grafikonok a funkciók, és a közvetlen és.
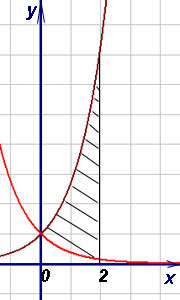
Határozat. Mivel a [0, 2]. Ezután a következő képlet segítségével megtalálásához a területet (3), megkapjuk
10. példa Keresse meg a területet a szám, és arra a következtetésre jutott közötti parabola.
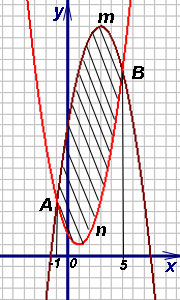
Határozat. AmBn kiszámításához szükséges területet az ábra. amelyben az oldalsó szegmensekhez degenerálódott, hogy az A pont és a kereszteződés B parabola. Megoldása (szükség szerint) parabola egyenlete, azt látjuk, hogy abszcissza és. A intervallum [-1, 5] kapjuk. Ezért a (3) képlet találunk a területen az ábra:
11. példa Find a terület az ábrán, között kötött egy parabola és egy egyenes vonal.
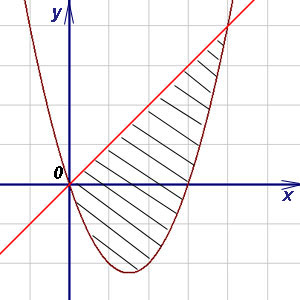
Határozat. Találunk abszcisszájának metszéspontjai egy parabola és egy egyenes vonal, és. Mivel a [0, 4]. A (3) képlet találunk a területen az ábra: