Kényszerrezgés és rezonancia
Amennyiben egy test egy m tömegű vannak rugalmas erő Fy = -kX, a súrlódási erő
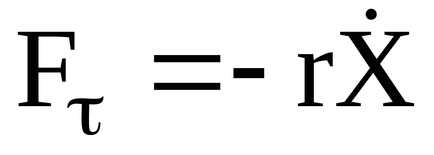
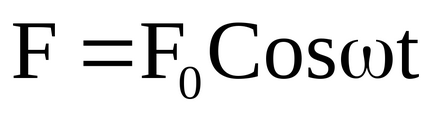
ahol
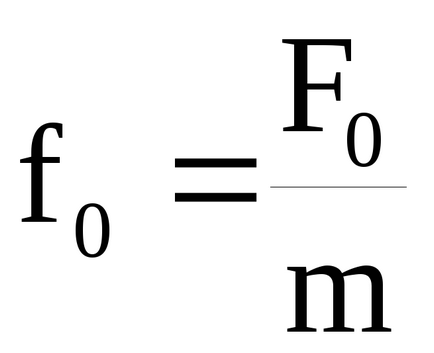
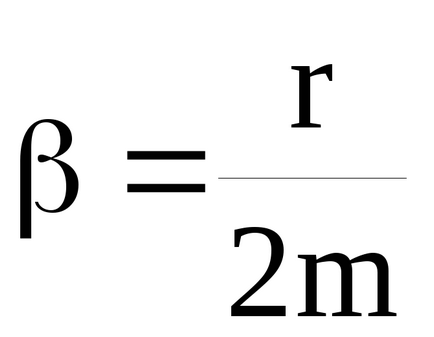
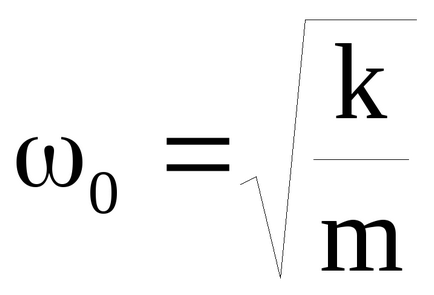
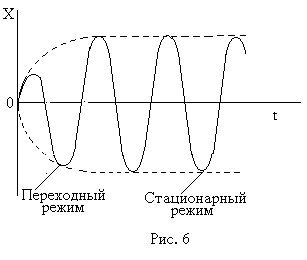
Még mindig tele van energiával által kifejtett külső erő nem lesz teljesen töltött leküzdésében súrlódás, amely egyenesen arányos a sebesség. Ezért egyensúly jön létre, amelyben az összeg mozgási és helyzeti energia állandó. Ez az állapot jellemzi az állandósult a rendszer.
Ebben az állapotban, mozgás a test lesz harmonikus frekvenciájú egyenlő a frekvenciát a külső gerjesztés, hanem azért, mert a tehetetlenség a rezgések el lesznek tolva fázisban viszonyított pillanatnyi értékének a külső periodikus erő:

Ellentétben szabad rezgési amplitúdójának A és fázisú kényszerített oszcilláció
nem függ a kezdeti feltételek a mozgás, és fogja meghatározni csak a tulajdonságait az oszcilláló rendszerhez, amplitúdója és frekvenciája a hajtóerő:
Látható, hogy az amplitúdó és a fáziseltolódás gyakoriságától függ a hajtóerő (ábra7 és 8).
A jellemző a jelenléte kényszerített oszcilláció rezonancia. Megjelenése erőteljes növekedése kényszerített oszcillációs amplitúdóját, amikor a frekvencia a hajtóereje, hogy természetes frekvenciája a test szabad, csillapítatlan rezgések ω0 nevezzük mechanikai rezonancia. A rezgés amplitúdója a test rezonanciájának
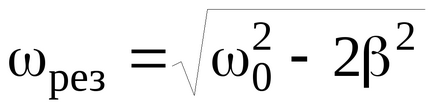
Ami a rezonancia görbe (lásd. Ábra. 7.), akkor a következő észrevételeket teszi. Ha ω → 0, akkor az összes görbe (lásd. Is (35)) jön ugyanazt a nem nulla, a határérték
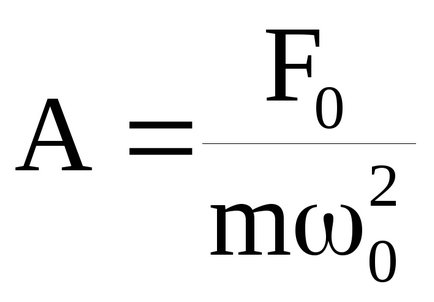
Feltéve, kis csillapítás (β 2 << ω0 2) rezonancia amplitúdója (cm. (37))
Ilyen feltételek mellett veszi a rezonancia offset kapcsolatban statikus elhajlás.
,
ami azt mutatja, hogy a relatív növekedése a rezgési amplitúdó rezonancia határozza meg a minősége a vibrációs rendszer. Itt a minőségi tényező lényegében válasz nyereség
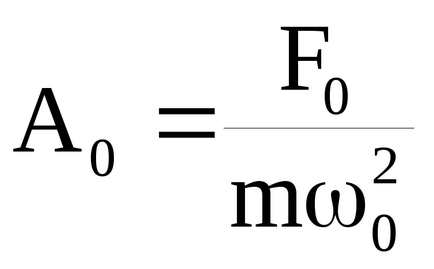
Ez a körülmény okozza rezonancia jelenség nagy jelentősége van a fizika és a mérnöki. Használni, ha akarják, hogy fokozza a rezgéseket, például az akusztika -, hogy fokozza a hang hangszer, rádió - válassza ki a kívánt jelet egy sor más különböző frekvenciákon. Ha a rezonancia mozhetprivesti kedvezőtlenül növeli dobemelés használt alacsony Q tényező.
A forrás a periodikus külső erő lehet a második rezgő rendszer, rugalmasan kapcsolódik az első. Mindkét oszcilláló rendszerek hatnak egymásra. Például, az esetben, ha két összekapcsolt ingák (ábra. 9).
A rendszer végezhet mind-fázisban (lásd 9B.), És az anti-fázis (9C.) Ingadozások. Az ilyen rezgések nevezzük normál típusú vagy normális rezgési módja és az jellemzi, hogy saját szokásos gyakorisága. Amikor a közös módusú előfeszítése támasztóingák rezgések minden időpontokban X1 = X2. ω1 és a frekvencia megegyezik a frekvencia egy inga
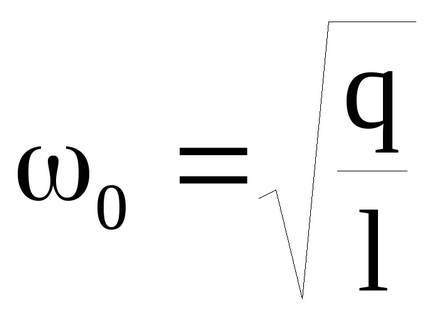
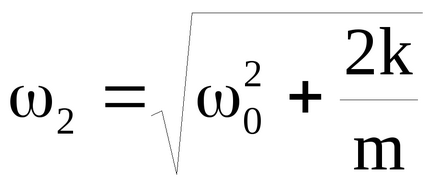
Bármely állam a mi kapcsolódó rendszerek, beleértve a kezdeti elmozdulás X (. Ábra 9a), reprezentálható szuperpozíciója két normál mód:
Ha ólom rendszer mozgásba a kezdeti állapot X1 = 0,
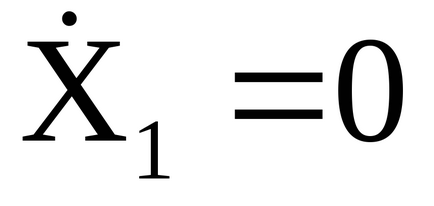
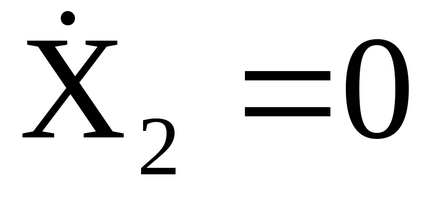
az inga elmozdulás által leírt kifejezések:
,
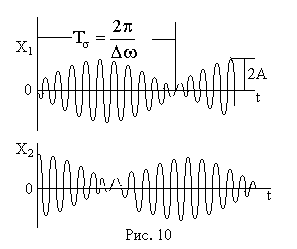
Pendulum rezgési frekvenciája megegyezik az átlagos gyakorisága a két normál mód
és azok amplitúdója változik, mint a szinusz a kúp, vagy kisebb gyakorisággal felével egyenlő a különbség gyakorisága szokásos módok
A lassú változás amplitúdója a frekvencia megegyezik a fele a normál üzemmód a frekvencia különbség, az úgynevezett „veri” a két rezgési frekvencia közel azonos. A frekvencia „veri” különbséggel egyenlő frekvencia ω1 -ω2, (és nem különbség felét), mivel a maximális amplitúdója 2A elért kétszer időszakban megfelelő frekvencia
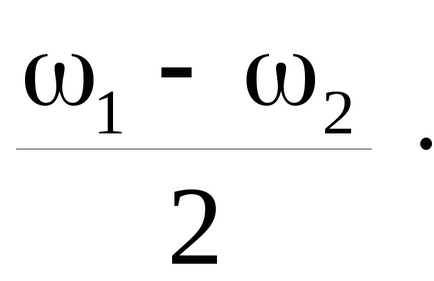
Ebből az időszakból egyenlő az ütemet
Ha ütés között inga energia cserélt. Azonban, egy teljes energia csere csak akkor lehetséges, ha a két tömegek azonosak, és az arány (ω1 + ω2 / ω1 -ω2) egy egész szám. Meg kell említeni egy fontos pont: bár az egyes ingák cserélhet energiát, a csere az energia a rendes mód áll rendelkezésre.
A jelenléte az ilyen oszcilláló rendszerek, amelyek kölcsönhatásba lépnek egymással és képesek kommunikálni egymással az energia, alapját képezik a hullám mozgás.
Oszcillációs anyagi test helyezzük egy rugalmas közegben, magával ragadja és hozza oszcilláló mozgást szomszédos részecskék a közegben. Jelenléte miatt a rugalmas kötések részecskék közötti jellegzetes oszcillációk terjednek a folyadék sebességének az egész közegben.
A folyamat a hullámterjedés rugalmas média úgynevezett hullám. Két fő típusa hullámok: hosszanti és keresztirányú. A longitudinális hullámok közepes részecskék rezeg iránya mentén a hullám terjedési, és keresztirányú - irányára merőleges hullámterjedés. Nincs olyan rugalmas közegben képes szaporodni átlós hullám. Keresztirányú elasztikus hullám csak akkor lehetséges, környezetben, amelyben a rugalmas nyírási alakváltozás. Például, a gázok és folyadékok kizárólag longitudinális rugalmas hullámok (hang).
A pontok helye a médiumban, amely ezen a ponton elérte az idő ingadozását az úgynevezett hullám előtt. A hullám előtt a tér elválasztja már részt vett egy hullám folyamat, a terület, ahol a rezgés nem történt. Attól függően, hogy a hullámfront alakja megkülönböztetni lapos, gömb, henger, stb
A egyenlete síkhullámú szaporítóanyag homogén veszteségmentes közeg formájában
ahol ξ (x, t) - elmozdulása a részecskék a közeg az X koordináta az egyensúlyi helyzetből t időpontban, A - amplitúdó,
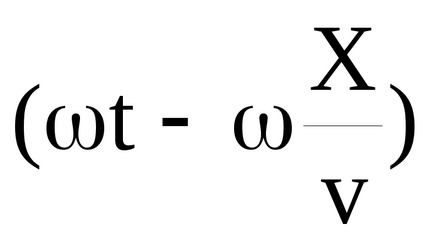
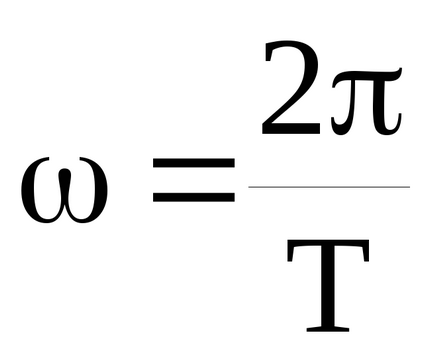
Hullámhossz λ a pontok közötti távolság, oszcillál a fáziskülönbség 2π, más szóval, a hullámhossz az úgynevezett útnak minden hullám fázisa az egyik időszakban oszcilláció:
A fázissebesség, azaz terjedési sebessége ebben a szakaszban:
A hullám száma - a hullámhosszak száma illeszkedő hosszúságú 2π egységek:
k = ω / v = 2π / λ. (45)
Behelyettesítve ezt a jelölést (42), az egyenlet egy sík futó monokróm hullám is képviselteti magát
Megjegyezzük, hogy a hullám egyenlet (46) érzékeli a kettős periodicitás a koordináta és az időt. Valóban, a fázisok a rezgések ugyanazok, mint a koordináta λ és
változás ideje T (időszak). Ezért grafikailag nem hullám síkjában. Gyakran fix idő t és a rajz képviseli a függését az elmozdulás a X koordináta ξ, azaz pillanatnyi eloszlását eredményezi az elmozdulás közeg részecskék iránya mentén hullámterjedés (11. ábra). A fáziskülönbség Δφ közepes pontok oszcillációk a távolságtól függ, AH = X2 - X1 ezen pontok között
Ha a hullám utazik irányával ellentétes X, a hátra hullámegyenlet írott formában:
ξ (x, t) = ASOS (ωt + Kx). (48)
Állóhullámok - az eredmény egy speciális típusú interferencia. Ezek kialakítva egymásra helyezésével két utazó hullámok szaporító ellentétes irányban azonos frekvenciájú és amplitúdójú.
Egyenletek két síkhullámok szaporító az X tengely mentén ellentétes irányban, hogy a forma:
Hozzáadása ezen egyenletek segítségével az összetételnek megfelelő mennyiségű koszinuszok és tekintettel arra, hogy k = 2π / λ, megkapjuk az egyenlet egy állóhullám
Módosítót cos ωt azt mutatja, hogy a közegben jelenik pont rezgésének ugyanazt a frekvenciát és az amplitúdó ω
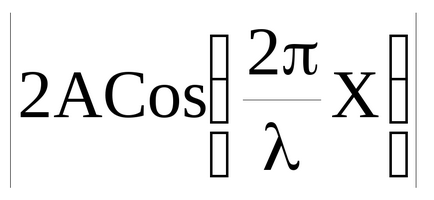
rezgésamplitúdót eléri a maximális értéket elérő 2A. Ezek a pontok az úgynevezett amplitúdópontok. A kifejezést (51) találunk koordinátáit amplitúdópontok:
A pontokon, ahol
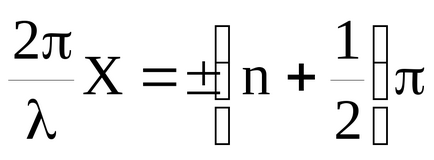
A rezgési amplitúdó nulla lesz. Ezek a pontok az úgynevezett csomópontok. A koordináták a csomópontok
P
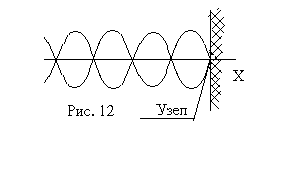
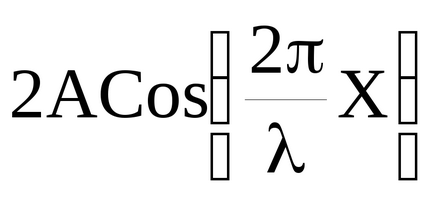
Eloszlás csomópontok és amplitúdópontok állóhullámban függ a fennálló feltételek a felület közötti két közeg, amelynek a reflexió lép fel. Ha hullámvisszaverődés zajlik a sűrűbb közeg, akkor a fázis a rezgés a helyszínen a gondolkodási hullám megfordul vagy, mondjuk, egy félhullámú elveszett. Ezért, ennek eredményeként a hozzáadásával oszcillációk ellentétes irányban eltolt határán nulla, azaz a összeszerelés történt (12.).

Az állóhullám egy fáziseltolódás, nincs hullámterjedés, nincs energiaátadás is, amely nevét az ilyen típusú hullámok.