Hogyan talál egy átlós keresztmetszeti területe

A átlója a kocka-szakasznak az alakja egy téglalap, amelynek területe (S) könnyen kiszámítható, ismerve a hossza az egyes borda (a) egy ömlesztett formájú. Ezt a téglalapot az egyik fél lenne a magassága, amely egybeesik élhosszúságú. A hossza a másik - az átlós - számítási a Pitagorasz tétel háromszög, amelyben ez a átfogója és a két alap széleit - a lábak. Általánosságban elmondható, hogy felírható: a * √2. A terület átlós részének keresse meg a szorzás a két oldalának a hossza, amit találtam: S = a * a * √2 = a² * √2. Például, ha a szélén egy 20 cm hosszú átlós keresztmetszeti területe a kocka kell kb 20² * √2 ≈ 565.686 cm.

Kiszámításához a keresztmetszeti területe az átlós a paralelepipedon (S) eljárni azonos módon, de megjegyezzük, hogy a Pitagorasz-tétel ebben az esetben részt a lábak különböző hosszúságú - a hosszúság (L) és szélességét (W) mennyiségi adatok. Átlós hossza ebben az esetben egyenlő lesz; ¥ (l² + w²). A magassága (h) is különböznek a hossza a széleit bázisok, így általános képletű keresztmetszeti területe a következőképpen írható fel: S = h * √ (l² + w²). Például, ha a hossza, magassága és szélessége a paralelepipedon rendre 10, 20 és 30 cm-es, a diagonális keresztmetszeti területe körülbelül 30 * √ (10² + 20²) = 30 * √500 ≈ 670,82 cm.

Az átlós részén négyszögletes piramis van egy háromszög alakú. Ha a magassága (H) a polihedron ismert, és annak bázis rejlik egy téglalap, a hossza a szomszédos élei (a és b), amelyek azonos körülmények között, a számítást a keresztmetszeti területe (S) kezdődik számítási az átlós hossza a bázis. Akárcsak az előző lépéseket használata a két széle a háromszög és a bázis átlós ahol pitagoreusi hossza átfogója egyenlő; ¥ (a² + b²). A magasság a piramisok poliéder egybeesik a magassága a háromszög az átlós részének. csökkentette az oldalon, amelynek hossza most definiált. Ezért, a megállapítás a háromszög területe kap a magasság felénél a terméket a hossza a diagonális: S = ½ * H * √ (a² + b²). Például, egy 30 cm magasságban, és a hossza a szomszédos oldalán a bázis 40 és 50 cm-es átlós keresztmetszeti területet kell közelítőleg egyenlő ½ * 30 * √ (40² + 50²) = 15 * √4100 ≈ 960,47 cm.

A szükséges hosszát. Használata általános képlet: Pyramid élhosszúságú egyenlő gyökér négyzetösszege különbségek a megfelelő koordinátákat a határ pont. Helyettesítő számok a koordinátákat a képlet, és megtalálja a hossza a széle a piramis. Ugyanígy kap a hossza a bordák nem csak a rendszeres piramis. de négyszögletes és csonka, és önkényes.

Keresse meg a hossza a bordák a piramis. amelynek minden élek egyenlő, a számadatokból bázis oldalán, és az ismert magasságot. Határozza helye magassága egy bázis, azaz az alsó pontot. Mivel a bordák egyenlő, így lehetséges, hogy rajzoljon egy kört, amely a metszéspontja az átlók a központ a bázis.

Döntetlen összekötő egyenes vonal az ellenkezője az alap sarkait a piramis. Jelölje meg azt a pontot, ahol metszik egymást. Ugyanez a pont, és lesz egy alsó határa a magassága a piramis.

Keresse meg a hossza az átlós a téglalapot a Pitagorasz-tétel, ahol a négyzetének összege a lábak a derékszögű háromszög egyenlő a tér a átfogója. Get a2 + b2 = c2, ahol a és b - a lábak, és - az átfogó. Ezután az átfogó egyenlő a négyzetgyök négyzetének összege a másik két oldala van.

Keresse meg a hossza a bordák a piramis. Először is, ossza el a átló hosszát felét. Minden vett adatértékeket, hogy helyettesítse a Pitagorasz fenti képletű. Hasonlóan az előző példához, hogy a gyökér a négyzetösszege magasságának és az átló fele a piramis.

• hogyan lehet megtalálni a élhosszúságú koordinátáit

Ez az úgynevezett axiális metszete, amely áthalad a geometriai tengelye a test által alkotott forgása bizonyos geometriai alakzat. A henger kapott körüli forgatás egyik a téglalap oldalai, és ezek miatt sok tulajdonságait. Formázás ez a geometriai test párhuzamosak és egyenlő egymással, ami nagyon fontos, hogy meghatározzák a paraméterek a tengelyirányú szakaszban, beleértve a átlósan.

• - henger előre meghatározott paraméterek;
• - papírból;
• - ceruza;
• - vonal
• - iránytű;
• - Pitagorasz-tétel;
• - tétele szinusz és koszinusz.

Construct szerinti henger előre meghatározott feltételek. Annak érdekében, hogy dolgozzon, meg kell tudni, hogy a sugár a bázis és a magasság. Azonban, más paraméterek is, amennyit a feladat meghatározás az átlós - például a szög között az átlós és alkotó vagy bázis átmérője. Ebben az esetben, ha létrehoz egy rajzot a méretét, hogy a beállított. A többi egy tetszőleges, és azt mutatják, hogy adott neked. Jelölje ki a tengely metszéspont és a bázisok olyan O és O”.

Draw tengelymetszetben. Ez egy téglalap két oldala, amelyek átmérője a bázisok és a másik két - a generátor. Mivel mind a formázó merőleges alapon mindketten magasból a geometriai test. Jelölje ki a kapott téglalap ABCD. Töltsön az AC átló és BD. Ne feledje, a tulajdonságait az átlók a téglalap. Ezek megegyeznek egymással, és fele-fele a metszéspont.

Tekintsük a háromszög ADC. Igaza van, mert a CD-kép a talajra merőleges. Az egyik láb egy alap átmérőjének, a második - alakítás. Az átló átfogója. Gondoljunk hogyan kell kiszámítani a hosszát minden átfogó egy derékszögű háromszög. Ez egyenlő a négyzetgyök négyzetének összege a másik két oldala van. Azaz, ebben az esetben d = √4r2 + h2, ahol d - átlós, R - a sugara a bázist, és a H - magassága a hengerben.

Ha a probléma nem adott a henger magassága, de meghatározott szög átlós tengelyirányú szakaszt egy bázissal vagy felhasználásával a szinusz vagy koszinusz-tétel. Emlékezzünk vissza, hogy az átlagos adatok a trigonometrikus függvények. Ez egy olyan kapcsolat az ellenkező vagy a csatlakozó meghatározott szögben lábat az átfogója, hogy te és megtalálható. Tegyük fel, hogy állítsa be a magasságot és a szög a CAD és az átlós a bázis átmérője. Ebben az esetben használja a szinusztétel, hiszen CAD szög ellenkező alkotója. Keresse átfogója d általános képletű d = h / sinCAD. Ha a sugár és a ugyanabban a szögben, használja a tétel a koszinuszok. Ebben az esetben, d = 2r / cos CAD.

Az Ugyanez az elv érvényes azokban az esetekben, ahol a megadott ACD szög a diagonális és a generátor. Ebben az esetben a szinusz tétel akkor használatos, amikor egy adott sugarú és koszinuszok - ha ismeri a magasság.

Construct felületi metszéspontjában összhangban a piramis-kiálló frontális síkban Σ (Σ2).
Először jelöljük ki a megfelelő pontok szakaszok, amelyek nélkül meghatározható kiegészítő metszetszintet.

Σ metszik alapsíkkal a piramis egy egyenes vonal 1-2. Megjegyzés pont 12≡22 - elölnézet ennek egyenes - és egy függőleges kapcsolat építik vízszintes előrejelzések 11,21 mindkét oldalán és a bázis A1C1 B1C1

Rib SA (S2A2) metszi a sík a piramis Σ (Σ2) 4. pontjában (42). A vízszintes vetülete a S1A1 bordák kap a csatlakozási pont 41.

3 ponton keresztül (32) végre, mint egy kiegészítő vágási sík vízszintes sík szintje T (T2). Ez párhuzamos a vetítés P1 sík, és egy olyan szakaszt egy felülete a piramis háromszög hasonló az alapja a piramis. A S1A1 E1 megjelöli azt az időpontot S1S1 - pont K1. Döntetlen vonalak az oldalakkal párhuzamosan a piramis bázis A1V1S1, és kap S1V1 határpont 31. pontokat összekötő 11, 21, 41, 31, megkapja a vízszintes vetülete a kívánt szakasz felülete piramis előre meghatározott síkban. Első vetítés szakasz egybeesik a vetülete a frontális síkban Σ (Σ2).

A S1A1 E1 megjelöli azt az időpontot S1S1 - pont K1. Döntetlen vonalak az oldalakkal párhuzamosan a piramis bázis A1V1S1, és kap S1V1 határpont 31. pontokat összekötő 11, 21, 41, 31, megkapja a vízszintes vetülete a kívánt szakasz felülete piramis előre meghatározott síkban. Első vetítés szakasz egybeesik a vetülete a frontális síkban Σ (Σ2).

Tehát a probléma megoldódik, haladva elve által talált pontokból egyidejűleg tartozó két geometriai elem - a piramis felülete és egy előre meghatározott vágási sík Σ (Σ2).

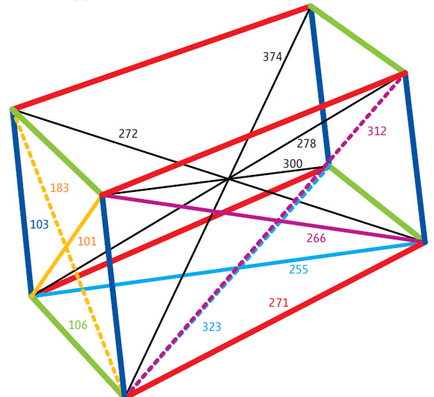
Próbálkozzon általánosabb problémát részletesen elemezni az építőiparban a keresztmetszet a kocka.
Hagyja, hogy a vágási sík metszésvonala meghatározott saját síkja és a sík, amely a kisebb alapja a doboz l és az a szög a sík p.
Az egész elve építési ábra szemlélteti.

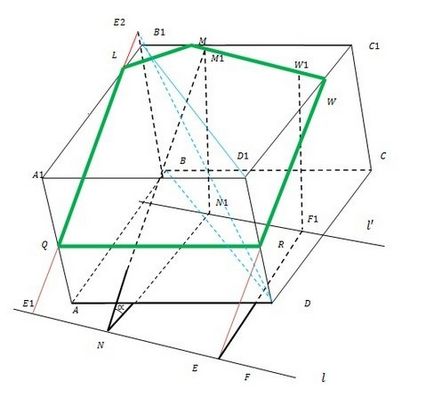
Határozat.
Bármilyen szög geometriai problémák konstrukció nem által meghatározott szöget, és annak bármely trigonometrikus függvény, legyen az kotangensét (CTG). Meg kell mérni bármely metrikus rendszer megoldás iránytű hossza Nctgf = d. Az érték mozgatása a skála a problémát, és azon az elven alapul a hasonlóság a derékszögű háromszögek egy közös hegyesszög, akkor a következő.

L a vonalon, hogy két tetszőleges pont N és F (tehát kívánatos, hogy minden további belül folytatni az alsó bázis ABCD kocka). Ezek közül a középső, felhívni ív sugarát d ABCD. Ezek az ívek ellop közös érintője l az keresztezi az AB és CD (továbbra is). érintse pont jel N1 és F1.

N1 és az F1 is fel kell vetnünk a függőlegesek M1 és W1 a felső bázis A1B1C1D1, amelynek hossza megegyezik N. Ezért a metszéspont nézni nem szükséges, bár ez elég egyszerű. Most kiterjeszteni M1W1 szegmens, hogy elnyomják a B1C1 és S1D1 az M és W volt. Tehát megtalálta az első oldalon a kívánt részt MW.

Ezután, a tartalmazó sík oldalfelület DCC1D1, húzzon egy vonalat a ponton W (E - az keresztezi az L egyenes vonal). WE keresztezi D1D - pont R. Cut WR - a második széle a kívánt részt.

Extend BB1 oldalsó éle a kocka az irányt a B B1. Az átlós síkja a kocka-szekcionált BB1D1D R ellop vonal az keresztezi egy kiterjesztése BB1 ​​pontban E2. Ebből az alsó sorban, hogy az keresztezi L E1. Közvetlen E1E2 metszi az oldalsó széleit a kocka és A1B1 AA1 pontokon L és Q, ill. Ezután ML, LQ és QR - további kívánt borda rész a kocka.

Sok tankönyvek talált munkahelyet építésével kapcsolatos szakaszok különböző geometriai formák, köztük a dobozt. Ahhoz, hogy megbirkózzon egy ilyen feladat, meg kell felfegyverkezve némi tudást.