Hogyan lehet megtalálni a legnagyobb közös osztója (GCD)
Tekintsük a két módszer a megállapítás a legnagyobb közös osztó.
Találni a módját, faktoring
Az első út áll megtalálni a legnagyobb közös osztó a számok adatok bomlás törzstényezős.
Ahhoz, hogy megtalálja a legnagyobb közös osztója Több szám elég, hogy őket prímszám, és szaporodnak egymás között, akik közös az összes ezeket a számokat.
1. példa Megtaláljuk a GCD (84, 90).
Felbontjuk a 84-es és a 90 törzstényezős:
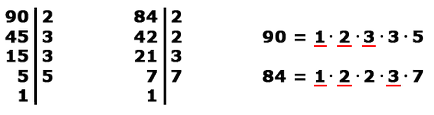
Tehát hangsúlyozta a közös prímtényezőknek, továbbra is szaporodnak össze őket: 1 · 2 · 3 = 6.
Így a GCD (84, 90) = 6.
2. példa Határozzuk meg GCD (15, 28).
Spread 15 és 28 törzstényezős:
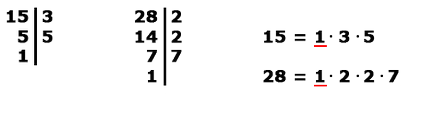
Numbers 15 és 28 viszonylag fix, mint a legnagyobb közös osztó - egységet.
Euklideszi algoritmus
A második módszer (különben ez az úgynevezett Euclid módszer) áll megtalálni a GCD egymást követő felosztása.
Először is vizsgáljuk meg ezt a módszert alkalmazzák csak két számot, és akkor meg kell érteni, hogyan kell alkalmazni, hogy három vagy több számot.
Ha a nagyobb a két szám van osztva adatok minimális száma, amely kisebb és a legnagyobb közös osztó.
1. példa: Vegyünk két szám 27 és 9. Mivel 27 osztva 9 és 9 osztható 9-cel, majd 9 közös osztója a számok 27 és 9. Ezt elválasztó egyidejűleg, és a legnagyobb, mert a 9 nem oszthatunk meg sorszáma nagyobb, mint 9. Ezért, a GCD (27, 9) = 9.
Más esetekben, hogy megtalálják a legnagyobb közös osztó két szám a következő eljárással:
- Két szám nagyobb mennyiségű adatra van osztva minimális.
- Ezután, egy kisebb számot elosztjuk a fennmaradó eredő részlege nagyobb számú kisebb.
- Továbbá, az első maradékot van osztva egy második maradékot, ami kiderült egy kisebb osztás száma az első maradékot.
- A második maradékot három, amelyeket veszünk az első osztály egy második maradékot, és így tovább. D.
- Így osztály mindaddig folytatódik, amíg az egyenleg nem nulla kapunk. Az utolsó osztó csak legyen a legnagyobb közös osztó.
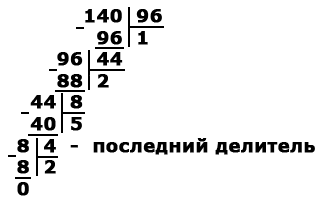
2. példa Keressük a legnagyobb közös osztó 140 és 96:
1) 140. 96 = 1 (44 maradék)
2) 96. 44 = 2 (maradékot 8)
3) 44. 8 = 5 (maradékot 4)
Utolsó osztó 4 -, ami azt jelenti, hogy a GCD (140, 96) = 4.
Az egymást követő osztás is rögzíthet oszlop:
- Először is, azt látjuk, a legnagyobb közös osztó bármely két szám több adatot.
- Majd találunk a GCD talált elválasztó és egy harmadik a számot.
- Akkor azt találjuk, az utolsó előfordulása NOD negyedik elválasztó és egy adott számot, és így tovább.
3. példa Találunk legnagyobb közös osztó 140, 96 és 48. A GCD szám 140 és 96, már megtalálható az előző példában (a 4-es számú). Továbbra is, hogy megtalálják a legnagyobb közös osztó 4-harmada ez a szám - 48:
48 osztva 4 maradék nélkül. Így a GCD (140, 96, 48) = 4.