Hogyan készítsünk egy mágikus négyzet

előző ◈ a következő

Számos különböző osztályozási mágikus négyzetek

ötödrendű, célja, hogy valahogy szervezni őket. A könyvben

a számot a főtér. Módszer érdekes, de nem több.

Hány hatodik érdekében terek még nem ismert, de ezek mintegy 1,77 x 10 19 száma hatalmas, így nincs remény megszámolni őket a teljes keresés, de a képlet a bűvös négyzetek lehetett gondolni.

Kitalált egy csomó módon építésének mágikus négyzetek. A legegyszerűbb módja annak, hogy mágikus négyzetek furcsa sorrendben. Az általunk használt módszer, amely azt javasolta, hogy a francia tudós, a XVII században A. de la Luber (De La Loubère). Ez alapján öt szabályt, amelynek hatása nézzük meg a nagyon egyszerű mágikus négyzet a 3 x 3 sejtekben.

1. szabály Put 1 a középső oszlopban az első sorban (ábra. 5.7).

Ábra. 5.7. Az első szám

Számú szabály 2. Ezután helyen, lehetőleg egy sejt szomszédos jelenlegi átlósan jobbra és fent (ábra. 5.8).

Hogyan készítsünk egy mágikus négyzet

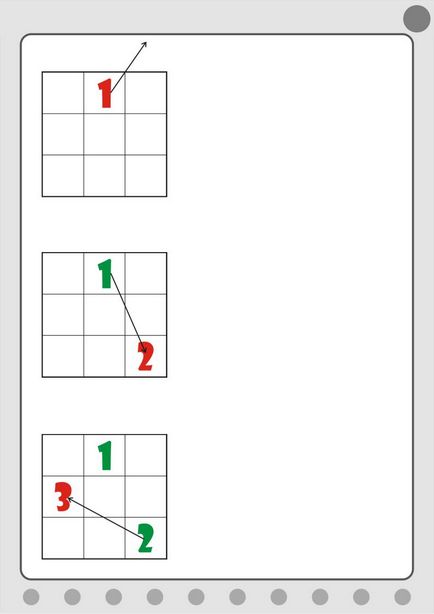
Ábra. 5.8. Igyekszünk, hogy a második szám

3. szabály: Ha az új sejt külső tér tetején. írja le a számot a legalsó sor és a következő oszlop (ábra. 5.9).

Ábra. 5.9. Azt hogy a második szám

4. szabály: Ha a cella kívül a téren, hogy a jobb oldalon. majd rögzítse a szám az első oszlop az előző sorban (ábra. 5.10).

Ábra. 5.10. Becoming a harmadik szám

Hogyan készítsünk egy mágikus négyzet

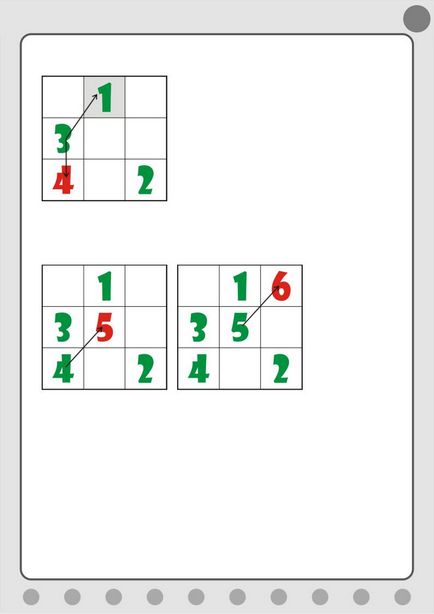
Szabály 5. Ha a cella már foglalt. majd egy másik rekord számú az aktuális cella (ábra. 5.11).

Ábra. 5.11. Mi tesz egy negyedik szám

Ezután lépni a 2. szabály (ábra. 5.12).

Ábra. 5.12. Tedd az ötödik és hatodik szám

Ismét, kövesse az utasításokat 3, 4, 5, nem kidolgozott az egész tér (Fig.

Hát nem, a szabályok nagyon sima és egyszerű, de mégis unalmas, hogy gondoskodjon még a 9 szám. Ugyanakkor, ismerve az algoritmus építésére mágikus négyzetek, akkor könnyen hozzárendeli a számítógép összes rutin munka, így magát, csak kreatív, hogy írni egy programot.

Hogyan készítsünk egy mágikus négyzet

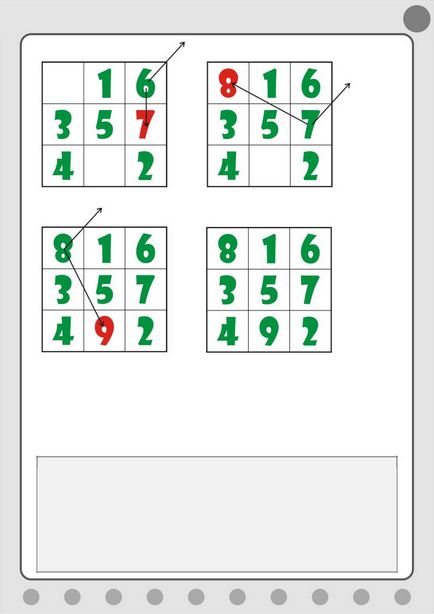
Ábra. 5.13. Töltsük a négyzet következő számokat

Project Bűvös négyzetek (Magic)

Mezőinek program Bűvös négyzetek kézenfekvő:

// programot hozunk létre

// ODD mágikus négyzetek

// MÓDSZER DE LA Lubero

állami részleges osztály Form1. forma

// max. négyzet mérete: const int MAX_SIZE = 27; // var

int n = 0; // érdekében a tér int [,] MQ; // bűvös négyzet

int szám = 0; // aktuális bejegyzések száma a négyzet

Hogyan készítsünk egy mágikus négyzet

int col = 0; // aktuális oszlop int sor = 0; // aktuális sor

Módszer de la Lubero előállítására alkalmas a páratlan négyzetek bármilyen méretű, így biztosítani tudjuk a felhasználó a képesség, hogy válassza ki a sorrendben a négyzet, ésszerű, miközben korlátozza a választás szabadsága 27-D sejtek.

Ha a felhasználó rákattint a féltve btnGen generálása gombra. btnGen_Click módszer létrehoz egy tömböt tárolni számokat és megy generálni módszer:

// nyomja meg a „Generate”

private void btnGen_Click (tárgy feladó, EventArgs e)

n = (int) udNum.Value;

mq = új int [n + 1, n + 1];

// Létrehoz bűvös négyzet: generál ();

Itt kezdődik cselekedni szabályai szerint de la Lubero és írjuk be az első számot - egy - a közepén az első cella a tér bar (vagy tömb, ha úgy tetszik):

// Létrehoz bűvös négyzet void generál ()

// első szám: szám = 1;

// első oszlop a szám - átlag: col = n / 2 + 1;

// karakterláncot az első napon - az első: sor = 1;

// vezetjük be egy négyzet: mq [sor, oszlop] = szám;

Most mi következetesen parkol a többi sejtek - kettőtől n * n:

// léphet a következő számot:

előző ◈ a következő