Funkciók meghatározott parametrikusan
Tekintsük referenciavonal a síkra, amelyben a változók x, y funkciók a harmadik változó t (ismert paraméter):
Minden egyes t értéke bizonyos intervallumban megfelelnek bizonyos értékeket x és y, a. Ezért, egy bizonyos ponton M (x, y) síkban. Amikor t tartományok feletti összes értéke a beállított intervallumban, akkor a pont M (x, y) leírja bizonyos vonalat L. Az egyenletek (2.2) nevezzük paraméteres egyenletek vonal L.
Ha egy függvény x = # 966; (t) az inverz T = F (x), akkor helyettesítjük ezt a kifejezést az egyenletben Y = g (t), kapjuk az y = G (F (x)), amely meghatározza az y függvényében x. Ebben az esetben azt mondjuk, hogy az egyenlet (2.2) meghatározza az y parametrikusan.
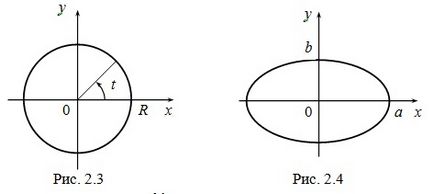
1. példa Legyen M (x, y) - tetszőleges pontja egy R sugarú kör, és az origó középpontú. Legyen t - közötti szög a tengely Ox és OM sugár (ld. 2.3.). Ha x, y expresszálódnak t:
Egyenletek (2.3) paraméteres egyenletek kerülete. Mi kizárják a egyenletek (2.3), a t paraméter. Ebből a célból, mind a egyenleteknek négyzet, és adjunk hozzá, kapjuk: x 2 + y 2 = R 2 (cos 2 t + sin 2 t), vagy x 2 + y 2 = R 2 - egyenlete egy kört a derékszögű koordináta rendszerben. Ez határozza meg a két funkció: Minden ilyen funkciók által adott paraméteres egyenleteket (2.3), de az első funkciót. és a második.
2. példa A paraméteres egyenlet
meghatározzák ellipszis, félig-tengelyei a, b (ábra. 2.4). Kiküszöbölése egyenletek t paraméter. Megkapjuk a kanonikus egyenlete ellipszis:
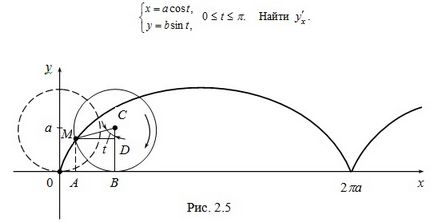
3. példa cikloist nevezett leírt vonal pont feküdt a kör, ha ez a kör tekercs csúszás nélkül az egyenes vonal (ábra. 2.5). Bemutatjuk azokat a paraméteres egyenleteket a ciklois. Hagyja, hogy a sugár a gördülő kör egyenlő a. pont M. leírja a ciklois, elején a mozgás egybeesik a származási.
Mi határozza meg a koordinátákat x. M y pont után a fordulási kör szögben t
(Ábra. 2.5), t = ÐMCB. MB ív hossza megegyezik a hossza a szegmens OB, mint kör tekercs csúszás nélkül, így
OB = at, AB = MD = ASINT, CD = acost, X = OB - AB = at - ASINT = a (t - sint),
y = AM = CB - CD = a - acost = a (1 - költség).
Így a kapott paraméteres egyenleteket a ciklois:
Ha a paraméter t 0 és 2π kerületének forog egy fordulattal, az M pont leír egy ciklois Arch. Egyenletek (2.5) beállítása függvényében y a x. Bár a funkciója X = A (t - Sint) van egy inverz függvény, de ez nem lehet kifejezni elemi függvényeken, úgy, hogy a függvény az y = f (x) nem lehet kifejezni elemi függvények.
Tekintsük származtatás függvény által adott paraméteres egyenlet (2.2). az x = # 966; (t) változások egy bizonyos intervallumban t az a inverz függvény t = f (x). akkor Y = g (F (x)). Legyen x = # 966; (t). y = g (t) származnak, ahol x't ≠ 0. A szabály szerint a differenciáló egy összetett függvény y'x = y't × T'x. A szabályok alapján differenciálódása inverz függvények. ezért:
Az így kapott általános képletű (2,6) lehetővé teszi, hogy megtalálják a függvény deriváltját meghatározott parametrikusan.
4. példa Legyen a függvény y. függően x. paraméterezett:
Határozat. .
Példa 5. Keresse meg a szögletes k együtthatót az érintő a ciklois pont M0. megfelelő paraméter értékét.
Határozat. Ország cikloist egyenletek: y't = ASINT, x't = a (1 - költség), ezért
A lejtőn a tangens ponton M0 az az érték, t0 = π / 4:
Legyen a függvény x0 ponton van egy származéka. A definíció szerint:
Ezért, a határérték tulajdonságok (Sec. 1.8). ahol a - amikor egy végtelenül # 916; x → 0. Ennélfogva,
# 916; y = f „(x0) # 916; x + # 945; × # 916; x. (2.7)
a # 916; x → 0, a második tag egyenletben (2.7) egy végtelenül magasabb rendű, összehasonlítva. ezért # 916; y és f '(x0) × # 916; x - egyenértékű végtelenül kicsi (ha f' (x0) ≠ 0).
Így a növekmény funkció # 916; y áll két kifejezések, amelyek közül az első f „(x0) × # 916; X egy növekménye a fő része # 916; y, egy viszonylag lineáris # 916; x (ha f „(x0) ≠ 0).
Differenciál f (x) x0 a fő része a növekmény funkció és jelöljük: dy vagy DF (x0). ezért
df (x0) = f „(x0) × # 916; x. (2.8)
1. példa Find a differenciál dy funkciót és a növekmény funkció # 916; y a függvény az y = x 2 által:
1) önkényes és X # 916; x; 2) X0 = 20, # 916; x = 0,1.
1) # 916; y = (x + # 916; x) 2x 2 = x 2 + 2x # 916; x + (# 916; x) 2x 2 = 2x # 916; x + (# 916; x) 2. dy = 2x # 916; x.
2) Ha x0 = 20, # 916; X = 0,1, majd a # 916; y = 40 × 0,1 + (0,1) 2 = 4,01; dy = 40 × 0,1 = 4.
Írunk az egyenlet (2.7) formájában:
# 916; y = dy + a × # 916; x. (2.9)
növekedés # 916; y dy eltérés különbözik egy infinitezimális a magasabb rendű, mint # 916; x, így hozzávetőleges számítás közelítő egyenlőség # 916; y ≈ dy, ha # 916; x eléggé kicsi.
feltéve, hogy # 916; y = f (X0 + # 916; x) - f (x0), megkapjuk a közelítő képlet:
Példa 2. Számítsuk kb.
Egyenletet használva (2,10), kapjuk:
.
Tehát ≈ 2,025.
Tekintsük a geometriai jelentése df (x0) a differenciális (ábra. 2.6).
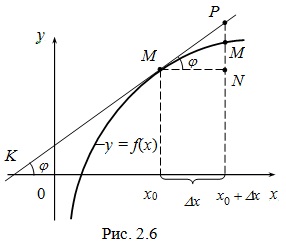
Rajzolásához függvény grafikonját y = f (x) érintőleges a ponton M0 (x0, f (x0)), hagyja # 966; - közötti szög az érintő és az KM0 Ox tengely, akkor f „(x0) = tg # 966;. -tól # 916; M0NP:
PN = tg # 966; × # 916; x = f „(x0) × # 916; X = df (x0). De PN fokozatosan összehangolja érintőleges változó x származó x0 x0 + # 916; x.
Következésképpen, a különbségi függvény f (x) x0 egyenlő a növekmény ordináta tangensét.
Találunk a differenciál függvény
y = x. Mivel (x) „= 1, akkor dx = 1 × # 916; X = # 916; x. Feltételezzük, hogy a differenciál a független változó x egyenlő a növekmény, azaz dx = # 916; x.
Ha x - tetszőleges számú, az következik (2,8) kapjuk df (x) = f „(x) dx, ahol.
Így a függvény deriváltját y = f (x) az aránya a differenciálzár a differenciál annak érv.
Tekintsük a tulajdonságok a differenciál funkciót.
Ha u (x), v (x) - differenciálható függvény, akkor a következő képlet:
Annak bizonyítására, ezek a képletek használják általános képletű összegére, a termék, és magán funkciókat. Megmutatjuk például képlet (2,12):
d (u × V) = (u × v) '# 916; X = (u × v' + u '× v) # 916; x = u × v' # 916; x + u „# 916; X × v = u × dv + v × du.
Tekintsünk egy komplex eltérés funkció: y = f (x), X = # 966; (t), azaz y = f (# 966; (t)).
hogy x't = dx, megkapjuk dy = y'x dx = f „(x) dx.
Így a differenciál függvény egy függvény y = f (x), ahol x = # 966; (t), adja meg a dy = f „(x) dx, ugyanaz, mint abban az esetben, ahol x a független változó. Ez a tulajdonság az úgynevezett differenciális alakja invariancia és.