derivált
A származékot (a funkció pontban) - az alapvető koncepciója egy differenciálszámítás, amely jellemzi az változási sebességét egy funkciót (az adott pontot).
A származékot (a funkció pontban) - az alapvető koncepciója egy differenciálszámítás, amely jellemzi az változási sebességét egy funkciót (az adott pontot).
A származékot úgy definiáljuk, mint a határérték az az arány a növekmény funkció a növekmény a paramétereként az érv növekmény, hogy 0, ha van ilyen határ. Egy függvény, hogy van egy véges származékot (egy bizonyos ponton), az úgynevezett differenciálható (ezen a ponton).
A folyamat a megállapítás a származék egy származtatása. A fordított folyamat - a számítás a primitív - integráció.
A fényképek fogalma származék:
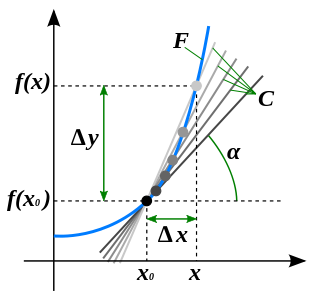
Tekintsük véletlenszerűen vett belső pontja x0 domain a függvény y = f (x).
Ahol a különbséget x - túl belső pont meghatározása, a növekmény az érvelés azon a ponton x0.
A különbség a növekmény a függvény x0 ponton. megfelelő távolsággal, és kijelölni.
Purinszármazékban funktsiiy = f (x) x0 a határa az arány a növekmény a növekmény az érvelés függvény ezen a ponton, mint az érv növekmény, hogy 0, ha van ilyen határ véges, azaz .:
A fő tulajdonságai a származékok.
Ha a pont x véges származékok függvények v = v (x) és u = u (x). akkor ezen a ponton vannak származékai az összeget. különbség, a termék és a hányadosa ilyen funkciókat is, ahol:
1. származékát az összetett függvény.
Ha a függvény az y = f (x) a származék a ponton x0. és az y = g (x) a származék pontban y0 = f (x0). majd komplex függvény h (x) = g (f (x)) is származik a ponton x0. ugyanakkor:
2. Az elégséges feltétele monoton.
Ha az összes pontot az intervallum (a, b) a következő egyenlőtlenség:
az y = f (x) növekszik ebben az intervallumban.
Ha az y = f (x) csökken (a; b).
3. A szükséges feltétele szélsőérték funkciót.
Ha a pont x0 egy extremális pontja a függvény y = f (x), és ezen a ponton a származék, miközben egyenlő 0:
4. Tünet maximum funkciót.
Ha a függvény az y = f (x) meghatározott intervallumban (a; b). folyamatos a ponton ez a származékos időközönként, és az intervallum és az intervallum, a lényeg x0 maximális pont a funkció:
5. Tünet legalább egy funkciót.
Ha a funkció határozza meg az intervallum, a folyamatos, azon a ponton, hogy a származékos időközönként, és az intervallum és az intervallum, a lényeg x0 a minimum pont a funkció:
Általában megtalálni a legnagyobb és legkisebb értéket a függvény.
Kiszámításához a legnagyobb és a legkisebb érték a függvény, amely az intervallum véges számú kritikus pont (pontok területén a megfordítására függvény deriváltját nullára, vagy nem létezik), akkor meg kell határozni a függvény értékei az egyes kritikus pont és a végpont, és válassza ki a legnagyobb és nyert kis számban.
Meghatározása származékot egy függvény.
Tegyük fel, hogy a szomszédságában a funkció határozza meg. Származéka, a funkció számát A. oly módon, hogy a funkció a környéken is képviselteti magát:
ha egy létezik.
Meghatározása differenciálhányados keresztül határt.
Tegyük fel, hogy a szomszédságában a funkció határozza meg. Függvény deriváltját a f pont a határ, ha létezik:
Hagyományos kijelölése differenciálhányados egy ponton.
Megjegyezzük, hogy az utóbbi gyakran jelöli a származék adott időben (az elméleti mechanika).
Geometriai és fizikai jelentése a származék.
A lejtőn az érintő.
Ha a függvény véges származékot egy ponton a környéken akkor lehet közelíthető egy lineáris függvény:
F függvény érintője egy bizonyos pontig. A számot hívják lejtő meredeksége, vagy az érintő.
A változás sebessége függvényében.
Hagyja, - a törvény egyenes vonalú mozgás. Akkor ez fejezi ki a pillanatnyi sebesség az időben. A második derivált kifejezi a pillanatnyi gyorsulás időpontban
Általában, a függvény deriváltját a funkciót fejezi változási sebessége a pontot, azaz a a sebességet a folyamat, amelynek leírása függőség
Példák a funkciókat.
- Let. Ezután, ha a
ahol jelöli az előjelet funkciót. És ha valami, és ezért nem létezik.