Boltzmann állandó

Boltsman Lyudvig (1844-1906) - a nagy osztrák fizikus és egyik alapítója a molekuláris kinetikus elméletét. A Boltzmann írásaiban molekuláris kinetikus elméletét először jelent meg egy működő, koherens fizikai elmélet. Boltzmann adta statisztikai értelmezése a termodinamika második törvénye. Ők egy csomó fejlesztése és támogatása az elektromágneses mező a Maxwell-elmélet. A versenyző a természet, Boltzmann szenvedélyesen védte hogy szükség van egy molekuláris értelmezése termikus jelenségek és vette a terhét a harci tanítás, hogy tagadja molekulák.
Egyenletben (4.5.3) belép aránya egyetemes gázállandó az Avogadro állandó R NA. Ez az arány megegyezik az összes anyagot. Ezt nevezik a Boltzmann állandó, tiszteletére Boltzmann, egyik alapítója a molekuláris kinetikus elméletét.
Boltzmann állandó jelentése:
Egyenlet (4.5.3) a Boltzmann állandó van írva a következő:
A fizikai értelmében a Boltzmann állandó
Történelmileg, a hőmérsékletet először be, mint egy termodinamikai mennyisége és mértékegysége lett beállítva, hogy - fok (lásd § 3.2.). Miután létrehozó kommunikációt az átlagos hőmérséklet a kinetikus energia a molekulák nyilvánvalóvá válik, hogy a hőmérséklet lehet meghatározni, mint az átlagos kinetikus energiája molekulák és kifejezni azt joule vagy erg, m. F. értékei T helyett adja meg az értéket a T * úgy, hogy
Így meghatározott hőmérséklet azzal a hőmérséklettel, fokban kifejezett, az alábbiak szerint:
Ezért Boltzmann állandó értéket lehet tekinteni, mint összekötő hőmérséklet, egységekben kifejezve az energia, hőmérséklet, fokban kifejezve.
Gáznyomás függőség a koncentráció és hőmérséklet létrehozásához a molekulák
Kifejezése E a (4.5.5) és a behelyettesítve képletű (4.4.10), kapjuk expressziós mutatja a gáz nyomása függőség a koncentráció és a hőmérséklet a molekulák:
Formula (4.5.6), ebből következik, hogy ugyanolyan nyomás és hőmérséklet a molekulák koncentrációja gázok ugyanaz.
Ezért Avogadro-törvény: azonos térfogatú gázok azonos hőmérsékleten és nyomáson, az azonos számú molekula.
Az átlagos kinetikus energiája transzlációs mozgása molekulák egyenesen arányos az abszolút hőmérséklettel. A koefficiens arányosság - Boltsmanak állandó = 10 -23 J / K - emlékezni.
§ 4.6. Maxwell eloszlás
Sok esetben a tudás egyes átlagértékek fizikai mennyiség nem elegendő. Például a tudás az átlagos emberi növekedési terv nem teszi lehetővé a kibocsátás ruházati különböző méretekben. Tudnunk kell, hogy a hozzávetőleges száma, a növekedés, ami egy bizonyos tartományon belül. Hasonlóképpen fontos tudni, hogy a molekulák száma, amelynek sebessége eltér az átlagtól. Maxwell először találtak, ezeket a számokat lehet meghatározni.
Annak a valószínűsége, egy véletlen esemény
A §4.1 már említettük, hogy a viselkedésének leírására a lakosság nagy molekulák J. Maxwell bevezette a valószínűsége.
Mint már hangsúlyoztuk, elvileg lehetetlen nyomon követni a változás sebessége (vagy momentum) egyetlen molekula hosszú ideig. Sem lehet pontosan meghatározni a sebességet a gázmolekulák egy adott időben. Makroszkopikus környezet, amelyben a gáz (egy bizonyos összeget, és a hőmérséklet), nem merülnek fel azzal az igénnyel, hogy bizonyos értékeket molekuláris sebességek. Speed molekula lehet tekinteni, mint egy véletlen változó, amelyben az adatok a makroszkopikus feltételek különféle értékeket vehet fel, mint bármely, a pontok száma 1-6 (arcok száma hat csont) eshet a dobott kocka. Megjósolni, hogy hány pontot tartoznak ebbe a dobott kocka, akkor nem. De a valószínűsége, hogy esni, mondjuk, öt pont meghatározni.
Mi a valószínűsége, hogy egy véletlen esemény? Legyen ez készített egy nagyon nagy számú vizsgálat (n - kockák számát dob). Ebben az esetben, az N „esetben fordult elő kedvező eredmény vizsgálatokban (m. E. elvesztése öt). Ezután a valószínűsége, hogy ez az esemény az arány az esetek száma kedvező eredmény a teljes vizsgálatok száma a feltétellel, hogy ez a szám a sok nagy:
A szimmetrikus csontok valószínűsége bármely kiválasztott pontok számát 1-6 egyenlő
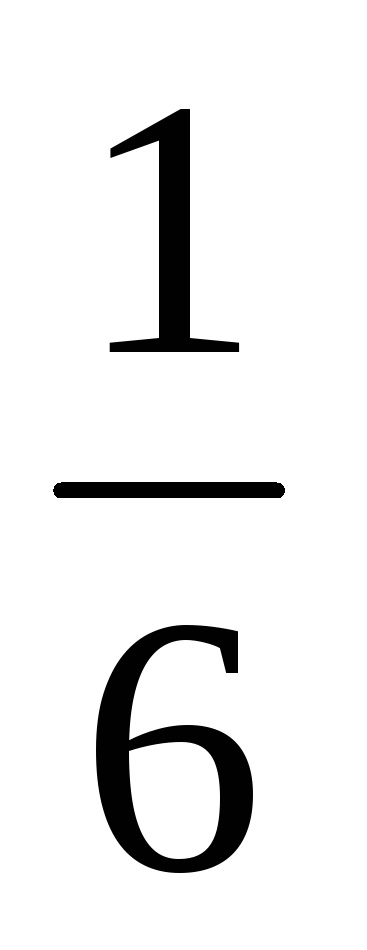
Látjuk, hogy egy bizonyos mennyiségi mintázat kimutatható a háttérben egy sor véletlenszerű események, a szám jelenik meg. Ez a szám - a valószínűsége - lehetővé teszi, hogy kiszámítja átlagok. Tehát, ha egy 300 dob a csontok, az átlagos kiessen az öt, az alábbiak szerint a képlet (4.6.1), egyenlő lesz: 300 ·
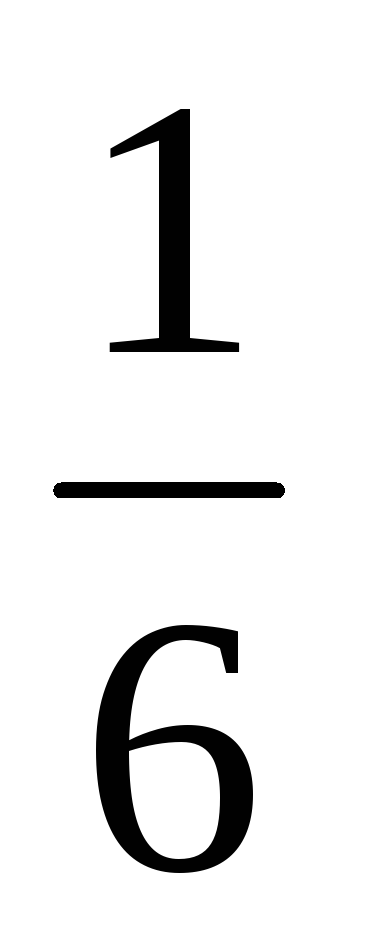
Kétségtelen, hogy a viselkedése gázmolekulák a hajó sokkal bonyolultabb mozgást dobott kocka. De akkor számíthat arra, hogy talál valami mennyiségi törvények alapján kiszámítható a statisztikai átlag, ha csak feltenni a problémát, valamint a játékelmélet, és nem úgy, mint a klasszikus mechanika. Szükséges, hogy hagyjon fel a megoldatlan probléma meghatározásának pontos értékét a sebessége a molekula a pillanatban, és megpróbálja megtalálni a valószínűsége annak, hogy ez az arány bizonyos jelentősége.