Az elemek a vektor elemzés
Zlementy vektor analízis
15.1. Vector területeken. Integrál és differenciális
jellemzőit vektormezők
15.1.1. Vector vonalak. differenciálegyenletek
vektor erővonalak
Definíció 1. A vektor mező egy része a tér (vagy az egész tér), ahol minden egyes pont M adott semmilyen fizikai jelenség, azzal jellemezve, hogy egy vektort mennyiséget.
Ha be a tér a derékszögű derékszögű koordináta-rendszert, a referencia vektor - mező funkciója csökken három nagyságrenddel skalár függvények:
A legegyszerűbb geometriai jellemzői vektor mezők vektor és vektorhoz vonal cső.
2. meghatározása vektor erővonalak nevezzük vonalak (görbék) minden pontban M ahol az érintő iránya egybeesik a mező irányát ezen a ponton.
Definíció 3. Vektor nevű cső felületén kialakított vektor vonalak pontokon átmenő fekvő mező egy zárt görbe, amely nem esik egybe (legalább részben) egy - line vagy vektor.
Ha a mező által megadott (1.1), az egyenlet a vektor vonalak kap egy rendszer differenciálegyenletek
Megjegyzés. Módszerek megoldására a rendszerek (1.2) (rendszerek szimmetrikus alakú) tekintik az elmélet differenciálegyenletek.
Definíció 4. Vektor mező úgynevezett lapos, ha speciálisan kiválasztott koordináta-rendszer, azt a formát:
A rendszer egyenletek (1.2) azoknak mezők a formája
és így a lapos térerősségvektor vonalak - kanyarodik fekvő párhuzamos síkban a sík Oxy.
1. példa Find a vektor mezőben (vektor = const; - a sugár vektor egy pont).
Határozat. Let; majd
.
Mi alkotják a differenciálegyenletek vonalak vektor rendszer (1.2):
.
Ez a rendszer a megoldási módja integrálható kombinációk. Az integrálható kombinációja szaporodnak a számláló és a nevező az első frakció az x. A második - y. a harmadik - a Z; adjuk hozzá a Terminusonként. Az ingatlan arányaiban megkapjuk
,
ahonnan kapjuk integrálható pályára :; integrálása, megkapjuk - az első integrált rendszer. Egy második integrálható kombinációs szorzatából a számláló és a nevező a frakció az első, a második - a, a harmadik - a; adjuk hozzá a Terminusonként megkapjuk
;
így tehát.
Így, a rendszer meghatározza, egyenletek kívánt vektor vonalak: a kör, amelyek központja a egy egyenesen átmenő származási irányába a vektor; A sík, amelyben fekszenek merőleges egyenes vonal.
Példa 2. Keresse meg a vektor mágneses erővonalak végtelen áramvezető.
Határozat. Hisszük, hogy a vezetőt tengelyének irányába Oz. és ugyanabban az irányban folyik. A vektor a mágneses mező által létrehozott áram, ahol - az áramvektor, - a sugár vektor egy pont; - távolság a tengelye a vezető előtt a pont előtt M. Van továbbá az egyenlet (1,2 ¢) formájában :, ahol - a vektor vonalak körök központja a tengely Oz.
15.1.2. Az áramlási mező vektort
1. meghatározása a vektor mező fluxust
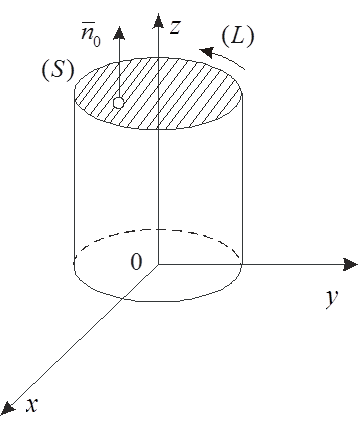
Nézzük a vektor mezőt, ahol a nyúlványok - folytonos függvények bizonyos régió (V). Tekintsünk egy sima (szakaszonként sima) kétoldalú orientált felületi (S) (azaz a kiválasztott kétoldalas felülete sík normális irányú).
Definíció. II anyagáram vektor területen keresztül kétirányú irányuló felületet (S) nevezzük felületi integrálja az első fajta a felület (ek):
Itt, - egységnyi vektor merőleges a kiválasztott oldalon (S); DS - felületének az elem (S).
Megjegyzés. Abban az esetben, egy zárt felület orientált kormányzott normális belsejében régió (V), a külső. Az oldalán a pozitív irányban a normál nevezzük pozitív oldala a felület.
A áramlás tud adni a belépés után át felületi integrálok az első és a második típus:
ahol - azaz - a vetítési terület Oyz síkon. Oxz. Oxy rendre.