Áttekintés ábrázolásával kvadratikus függvények
Annak érdekében, hogy felhívja a függvény grafikonját a derékszögű koordináta-rendszert, szükségünk van két merőleges vonal XOY (ahol O megelőző pont x és y), amelyek az úgynevezett „koordinátatengelyek”, és a mértékegység.

Annál a pontnál, két koordináta ebben a rendszerben.
M (x, y): M jelentése a neve a pont, x az abszcissza, és ez által mért Ox, és Y jelentése az ordináta és az arcok le Oy.
Két koordináta képviseli a távolság a lényeg, hogy a két tengely.

Ha figyelembe vesszük, az f függvény: A -> B (ahol A - dómén, B - terület függvény értékek), akkor a pont a grafikonon az ezt a funkciót lehet képviselve a formában a P (x, f (x)).
példa
F: A -> B, f (x) = 3x - 1
Ha x = 2 => F (2) = 2 × 3 - 1 = 5 => P (2, 5) a; Gf (ahol Gf egy grafikon, az ezt a funkciót).
másodfokú függvény
A szabványos formában: f (x) = ax 2 + bx + c
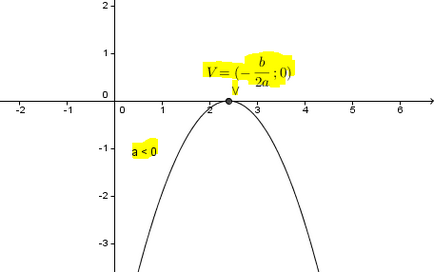
Ha a> 0, akkor a minimum érték az f (x) $ - \ frac $. amelyet úgy kapunk, ha a $ x = - \ frac $. Menetrend konvex parabola. Egy csúcs (az a pont, ahol irányt vált) a $ V (- \ frac - \ frac) $.
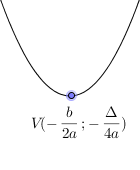

Ha egy <0. то минимальное значение f(x) будет $-\frac$. которое получается, если $x=-\frac$. Графиком будет вогнутая парабола. вершина которой это$V(-\frac;-\frac)$.
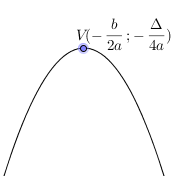

Parabola szimmetrikus olyan egyenes, amely áthalad a $ x = - \ frac $ és az úgynevezett „szimmetria tengelye”.
Ezért van az, amikor hozzá znayacheniya x. A vibiraem őket szimmetrikus $ - \ frac $.
Ha ábrázoljuk, metszéspontja a koordináta-tengelyek nagyon fontos.
|. Egy pont található a Ox tengely formájában P (x, 0). mert a távolság, amellyel az a Ox egyenlő 0 Ha a pont található, az Ox és a grafikon funkciót, ez is a formában a P (x, f (x)) → f (x) = 0.
Így annak érdekében, hogy megtalálják a koordinátákat a metszéspont a tengely Ox. meg kell oldani az egyenletet f (x) = 0. Kapunk az egyenlet egy 2 + bx + c = 0.
A döntés attól függ, a jel az egyenlet δ = b 2 - 4ac.
Immem az alábbi lehetőségek közül:
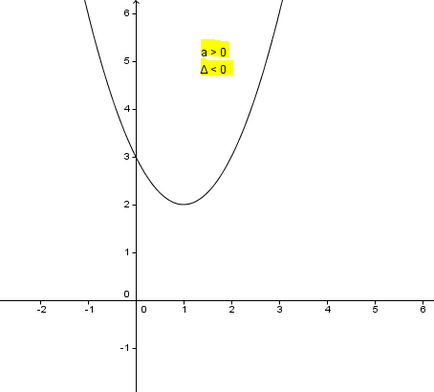
1) δ <0 ,
akkor nincs megoldás az egyenlet R (a valós számok halmazán), és a grafikon metszi Ox. Alakja a gráf:


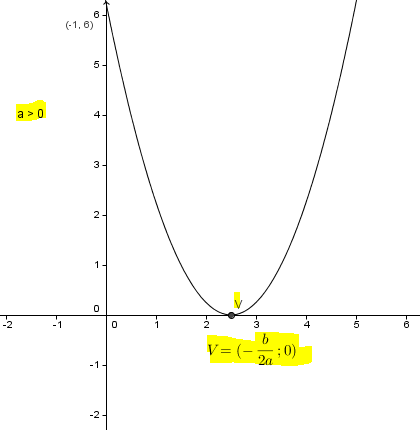
2) δ = 0,
majd két egyenlet megoldásai $ x_1 = x_2 = - \ frac $
Ami a menetrend tengely Ox a csúcsa a parabola. Alakja a gráf:


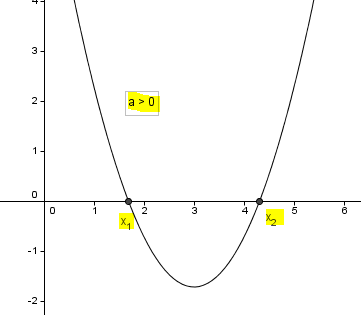
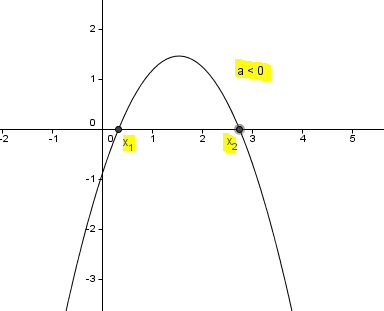
3) δ> 0,
akkor az egyenlet két különböző megoldást.
A grafikon a Ox tengely metszéspontjai M (x 1, és Ox keletkezik formájában .:


||. Egy pont a Oy tengely formájában R (0, y). mert a távolság Oy 0. Ha a pont található, az Oy és a gráf függvénnyel, ez is az űrlap R (x, f (x)) → X = 0 → R (0, F (0)).
Abban az esetben, a másodfokú függvény,
f (0) = a × 0 + b × 2 0 + c → R (0, c).
Szükséges lépéseket a grafikon egy másodfokú függvény
f: R → R
f (x) = ax 2 + bx + c
1. táblázatot változók, ahol sodródik néhány fontos az x értékét.
2. Számoljuk a koordinátákat a vertex $ V (- \ frac - \ frac) $.
3. Szintén levelet 0 az asztalra, és a null értékek szimmetrikus $ - \ frac $.
4. Meghatározzuk a metszéspont a tengellyel Ox megoldása az egyenletet f (x) = 0, és rekord x1 és x2 gyökerek a táblázatban.
δ> 0 →
δ <0 → точек пересечения нет. В этом случае мы выберем два удобных значения, которые симметричны $-\frac$
δ = 0 → ütemezés vonatkozik Ox közvetlenül a csúcsa a parabola. Ismét választani két kényelmes értékeit szimmetrikus $ - \ frac $. Mert tudjuk választani másik pár x értéke jobban meghatározzák az alak a gráf. de szimmetrikusan kell $ - \ frac $.
5. Azt, hogy ezeket az értékeket a koordináta-rendszerben, és szerkesszük meg a diagrammot csatlakoztatásával ezeket a pontokat.
1. példa
f: R → R
f (x) = x 2 - 2x - 3
a = 1, b = -2, c = -3
δ = b 2 - 4 × a × c = (-2) 2 - 4 × 1 × (-3) = 16
$ - \ frac = \ frac = 1 $ → V (1; 4)
2. F (0) = -3
Szimmetrikus 0, értéke 1 jelentése 2.
f (2) = -3
A grafikon fog kinézni:

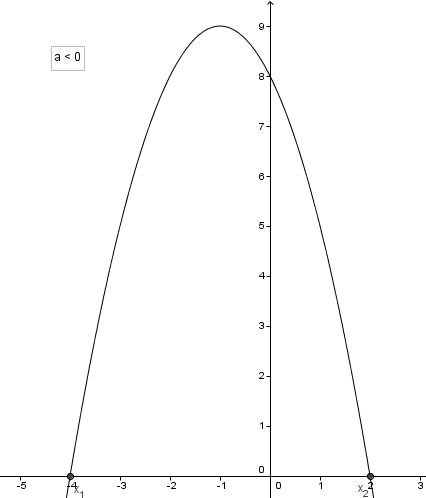
2. példa
f: R → R
f (x) = -x 2 - 2x + 8
a = -1, b = -2, c = 8
δ = b 2 - 4 × a × c = (-2) 2 - 4 × (-1) × 8 = 36
$ - \ frac = \ frac = -1 $ → V (-1; 9)
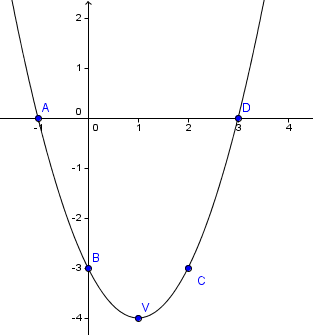
2. F (0) = 8
f (-2) = 8 (szimmetrikus értéke 0 egyenlő -1 -2)
A (-4; 0)
B (-2; 8)
V (1; 9)
C (0; 8)
D (2, 0)

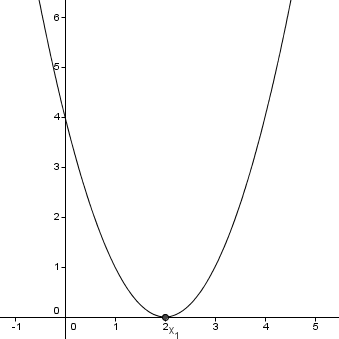
3. példa
f: R → R
f (x) = x 2 - 4x + 4
a = 1, b = -4, c = 4
δ = b 2 - 4 × a × c = (-4) 2 - 4 × 4 × 1 = 0
$ - \ frac = \ frac = 2 $ → V (2, 0)
2. F (0) = 4
f (4) = 4 (szimmetrikus értéke 0 4 2)
A (-2; 9)
B (0, 4)
V (2, 0)
C (4, 4)
D (5, 9)

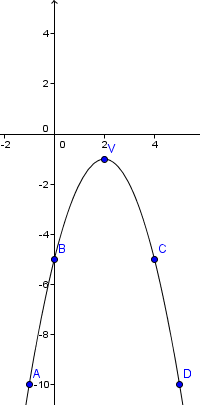
4. példa
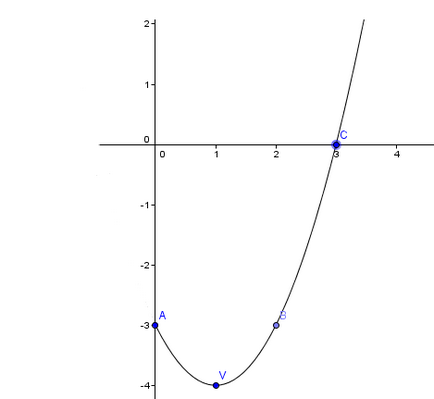
f: R → R
f (x) = -x 2 + 4x - 5
a = -1, b = 4, c = -5
δ = b 2 - 4 × a × c = február 04-04 × (-1) × (-5) = 16-20 = -4
$ - \ frac = \ frac = 2 $ → V (2, -1)
2. F (0) = -5
f (4) = -5 (szimmetrikus értéke 0 4 2)
3. f (x) = 0 → -x 2 + 4x - 5 = 0, δ <0
Ez egyenletnek nincs megoldás. Azért választottuk a szimmetrikus értéke körülbelül 2
A (-1; -10)
B (0, 5)
V (2, -1)
C (4; 5)
D (5, -10)

Ha a tartomány nem R (a valós számok halmaza), és néhány intervallum, akkor törli a grafikon részei, amely megfelel azoknak az x, amelyek nem ebben a tartományban. Meg kell rögzíteni az intervallum végpontjait a táblázatban.
5. példa
F: [0; + ∞) → R
f (x) = x 2 - 2x - 3
a = 1, b = -2, c = -3
δ = b 2 - 4 × a × c = (-2) 2 - 4 × 1 × (-3) = 16
$ - \ frac = 1 $ → V (1; 4)
2. F (0) = -3
f (2) = 0, a értéke -3 szimmetrikus 1 értéke 2)
3. f (x) = 0 → x 2 - 2x - 3 = 0, δ = 16
x1 = -1 ∉ [0; ∞)
x2 = 3
A (0, -3)
V (1; 4)
B (2; 3)
C (3, 0)