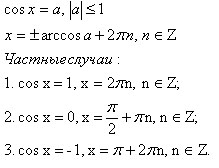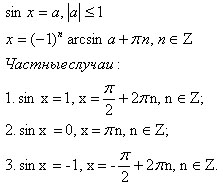A trigonometrikus képlet, az átalakítás a trigonometrikus függvények a kettős szög képletű
Az arány mértéke között és a szög radiánban intézkedések
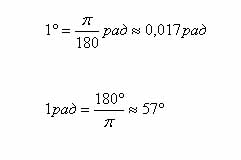
Definíciók:
A trigonometrikus függvények akut szögek lehet meghatározni, mint az arány a oldalainak hossza a derékszögű háromszög.
Szinusz és koszinusz az a szög meghatározható bármilyen szöget α. A tangens definiált összes értéket a szög α, kivéve a α = π / 2 + πn (a = 90 ° -ban + 180 ° * n), n = 0, +/- 1, +/- 2 kotangensét definiált összes értéket a szög α, α, kivéve = πn (α = 180 ° * n), n = 0, +/- 1, +/- 2.
Funkció sin α. cos α, szek α COSEC α, és van egy időszak 2π, és a funkciók és tg α CTG α - időtartamra π:
sin (α + 2πn) = sin α; COSEC (α + 2πn) = COSEC α;
cos (α + 2πn) = cos α; sec α + 2πn) = sec α;
tg (α + πn) = tga;
CTG (α + πn) = CTG α; n = 0, +/- 1, +/- 2.
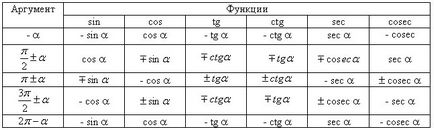
Kiszámítása értékeit trigonometrikus függvények bármely szög csökken az értékek kiszámítása során a trigonometrikus függvények a hegyesszögben a következő szabályok szerint:
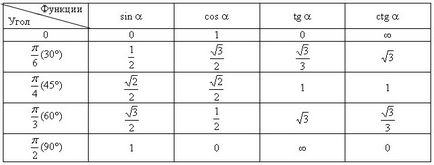
Néhány értékeit trigonometrikus függvények
Alapvető trigonometrikus azonosságok
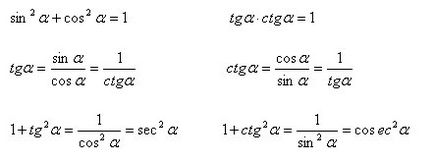
Páros vagy páratlan trigonometrikus függvények
F (x) függvény, még akkor is, ha az F (-x) = f (x).
F (x) függvény, páratlan ha F (-x) = - F (X).
F (x) függvény, vagy egy páros vagy páratlan minden más esetben.
sin α, tg alfa, CTG alfa és COSEC alfa - páratlan funkciókat.
sin (- α) = - sin α tg (- α) = - tg α; CTG (- α) = - CTG α; COSEC (- α) = - COSEC α.
cos α és sec α - még funkciót.
cos (- α) = cos α; sec (- α) = sec α.
Trigonometrikus függvények összegének és a különbség a szögek
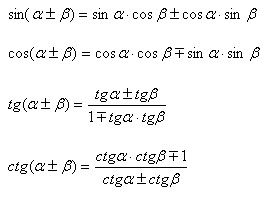
Expression sinα, cosa, tga keresztül TG (α / 2)
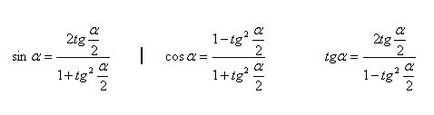
A kifejezés a néhány trigonometrikus függvények más

Trigonometrikus függvények a kettős, hármas és fél szögek

A fél-szög képletek jelek előtt gyökök venni attól függően, a jel a trigonometrikus funkció a bal oldali.
Mind a képletek az érintő kotangensét érvényes csak azzal a feltétellel, hogy minden funkciója értékek léteznek.
Konvertálása összeg (különbség) a trigonometrikus függvények munka (átalakítása trigonometrikus kifejezések olyan formába kényelmes logaritmálás).
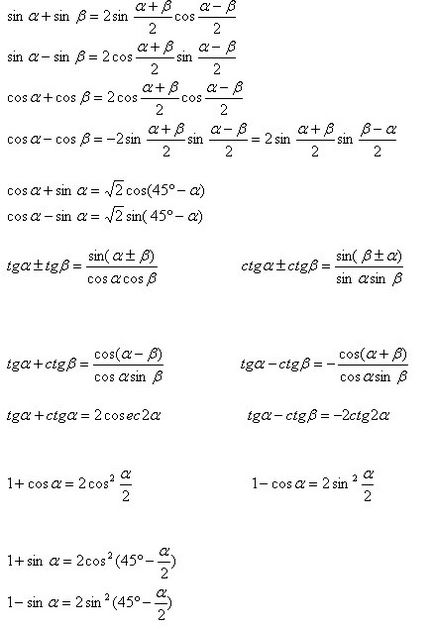
Conversion termékek trigonometrikus függvények összege.
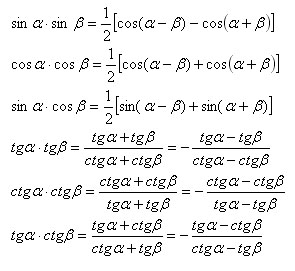
A jobb és bal oldalán az egyes általános képletű, amely magában foglalja az érintő és (vagy) kotangensét léteznie kell egyszerre.
A legegyszerűbb összefüggés az inverz trigonometrikus függvények.
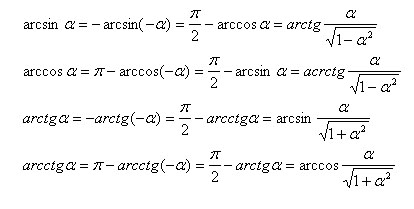
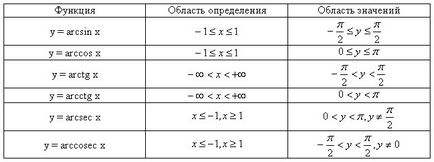
Megoldás trigonometrikus egyenletek.