A szög a sorok között - studopediya
A szög a két egyenes között a térben lesz az úgynevezett bármely szomszédos által bezárt szögek két vonal át húzott párhuzamos adatokat a tetszőleges pont.
A tér két vonalat:
Nyilvánvaló, hogy a sarokban # 966; A sorok között vehet a szög közötti irányvektorokkal és. Ettől. A képlet a koszinusza közötti szög a vektorok kapjunk
.
Feltételek párhuzamos és merőleges a két egyenes vonalak egyenértékű feltételeinek párhuzamos és merőleges a irányvektor és:
Két egyenes párhuzamos, akkor és csak ha a megfelelő együtthatók arányos, vagyis L1 L2 párhuzamos akkor és csak akkor, ha a párhuzamos.
Két sor merőlegesek, ha, és csak akkor, ha az összeg a termék megfelelő együtthatók nullával egyenlő :.
A szög az egyenes és a sík
Hagyja, hogy a vonal d - nem merőleges a síkra # 952 ;;
d „- a nyúlvány a síkra vonal d # 952 ;;
A legkisebb a szögek a sorok között D és D „hívjuk a szög a vonal és a gépet.
Jelölje meg a # 966; = (d, # 952;)
Ha d ⊥ # 952;. majd (d, # 952;) = π / 2
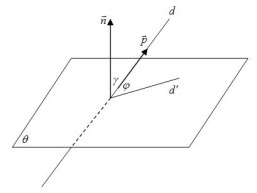
Oi → j → k → - derékszögű koordináta-rendszert.
Az a sík egyenletét:
Úgy véljük, hogy a vonal munkapont és az irányvektor: d [M 0, p →]
A vektor N → (A, B, C) ⊥ # 952;
Ezután továbbra is, hogy meghatározza a szöget vektorok között n → és p →, jelöljük azt # 947; = (n →, p →).
Ha a szög # 947;<π/2. то искомый угол φ=π/2−γ .
Ha a szög # 947;> π / 2. majd a kívánt szöget # 966 = # 947; -π / 2
Ezután, a szög között az egyenes vonal és a sík lehet kiindulni, amelyet a képlet:
Vopros29.Ponyatie négyzetes formában. Bejelentkezés meghatározottsága kvadratikus formák.
Kvadratikus alak j (x1. X2. ..., xn) n valós változók x1. x2. ..., xn az összege formájában
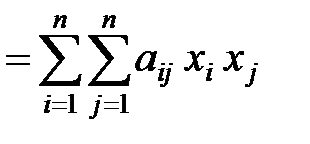
ahol aij - néhány számot, az úgynevezett együtthatók. Az általánosság elvesztése nélkül, akkor feltételezhetjük, hogy aij = aji.
A másodfokú formáját nevezzük érvényesnek, ha aij Î GR. A mátrix a kvadratikus alak egy mátrixot annak együtthatók. Kvadratikus alak (1) megfelel egy egyedi szimmetrikus mátrix
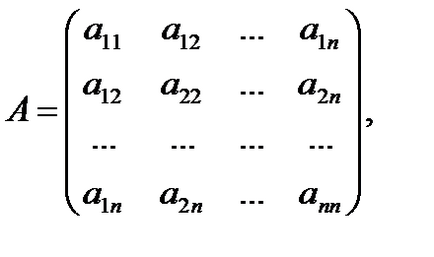
Ezzel szemben bármely szimmetrikus mátrix (2) megfelel a kvadratikus formájában csak legfeljebb jelölésére változók.
A rangsorban a kvadratikus formát nevezik rangot annak mátrix. A kvadratikus alak úgynevezett nem degenerált ha nonsingular mátrix A (Emlékeztetünk arra, hogy az A mátrix nonsingular ha determinánsa nem nulla). Egyébként kvadratikus alak degenerált.
A kvadratikus alak (1) pozitív definit (vagy erősen pozitív), ha
A pozitív definit kvadratikus alak j (x) szintén azt mondják, hogy a pozitív határozott. Következésképpen, a pozitív határozott kvadratikus alak megfelel csak a pozitív definit mátrix, és fordítva.
A kvadratikus alak (1) van meghatározott negatív (vagy szigorúan negatív), amennyiben
Hasonlóképpen, mint a fenti, negatív definit mátrix quad-kvadratikus formák is nevezik negatív határozott.
Következésképpen, a pozitív (negatív) definiált Quadra-ung formájában j (x) elér egy minimális (maximum) értékek j (x) = 0 x = (0, 0, ..., 0).
Megjegyzendő, hogy a legtöbb négyzetes formák nem biztos jele, vagyis ők sem pozitív, sem negatív. Ilyen négyzetes formák alkalmazni 0, nemcsak a származás, hanem más helyszíneken.
Ha n> 2, igényel speciális szempontok érvényesítésére bejelentkezési meghatározottsága kvadratikus formák. Nézzük őket.
Principal kiskorúak egy másodfokú forma az úgynevezett minor:
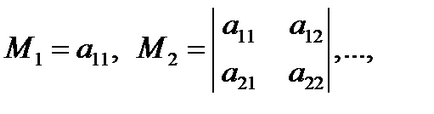
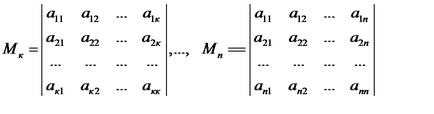
azaz, ez kiskorúak a sorrendben 1, 2, ..., n a mátrix A. található, a bal felső sarokban, amelyek közül az utolsó egybeesik a meghatározója a mátrix A.
Kritérium pozitív meghatározottsága (Sylvester kritérium)
A kvadratikus alak j (x) = x T Ax pozitív definit, szükséges és elégséges, hogy az összes fő kiskorúak A mátrix pozitív, azaz: M1> 0, M2> 0, ..., Mn> 0. Criterion a negatív bizonyosság annak érdekében, hogy a kvadratikus alak j (x) = x T Ax negatívan meghatározva, szükséges és elégséges, hogy fő kiskorúak pozitívak is rend és páratlan - negatív, azaz M1 .. <0, M2> 0, M3 <0, …, (–1) n