A problémák megoldását a témában - Piramis
A böngészője nem támogatja az iframe!
Lecke célja:- iskolai:
- Azt vizsgálja meg a emlékezeterősítő eszköz;
- levezetéséhez képletek fő átmenetet szögek a jobb piramisok;
- megtanulják, hogyan kell használni egy emlékeztető eszköz bizonyítani közötti kapcsolatok szögek a jobb piramis és megoldani a problémákat.
- fejlődő:
- fejleszteni a kognitív érdeke a képességek fejlesztésének, a kutatási diákok;
- fejleszteni alakú memória, absztrakt és logikus gondolkodás;
- hogy fejlessze a hallgatók számítógépes ismeretek.
- iskolai:
- oltásra kommunikációs készségek, a módszertani anyagok készségek (tájékoztatót, elektronikus forrás);
- generál pontos végrehajtását tevékenységek elvégzése gyakorlati munka és a csoportos munkát.
- számítógép
- projektor,
- képernyőn,
- interaktív tábla, a SMART Board,
- kiosztás
I. Szervezeti kérdések
- Kérem, nyissa ki a notebook, és írja le a számot, és a lecke téma: problémák megoldása a „piramis”. Ma az osztályban vagyunk megoldani a problémákat megtanulják, hogyan kell alkalmazni az egyéni vétel, úgynevezett emlékeztető. Levezetjük a képletek az átmenet alapvető szögek a jobb piramisok és megtanulják, hogy alkalmazza őket a problémák megoldásában.
- Ehhez meg kell ismételni néhány kérdésre a pályáról a geometria.
Orális munka (frontális felmérés).
Dan derékszögű ABC háromszög.

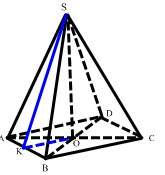
- Mi poliéder hívják piramisjáték?
- Melyek a piramis csúcsára? Alapítvány?
- Mi piramis úgynevezett jobb?
- Amennyiben vetített magassága szabályos piramis?
- Név közötti szög az oldalsó széle és az alapja a piramis; Között az oldalsó felület és egy bázis; közötti szög az oldalfelületek a piramis?
Tekintsük a probléma megoldása egy tankönyv. Figyelem a fedélzeten.
№ 255. A szabályos háromoldalú piramis bázis oldala 8 cm, és a lapos csúcsszög egyenlő, hogy a magassága a piramis.
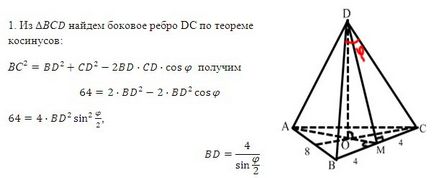
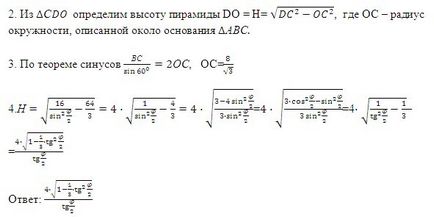
III. Kialakulását az új ismeretek
A probléma megoldása érdekében meg kellett küzdenie a háromszögek, amelyek nem egy síkban fekszik, és mi több, mindegyikük ismert volt, hogy nem több, mint két elem. Mit gondol, van-e a matematika egyszerűbb módja annak, hogy megoldja a problémát? Azt állítják, hogy ott van! Valóban, egy ilyen eljárás létezik. És van egy név emlékeztető megoldani geometriai problémákat. Tőle, hogy én mutassam be ma. Tehát ...
Mnemonic (a görög - memória) - egy másfajta technikát, amelyek elősegítik a mesterséges megjegyezni. Más szóval - ez a művészet memorizálása. Már az ókori népek és vadak ismert számos technikát, aki adta pontot memória csapágy. Azt is tudjuk, néhány emlékeztető módszerekkel, például tárolása a szivárvány színei, a meghatározása a felezővonal és mások.
Tehát, egy emlékeztető eszköz <Приложение 3> A függőség szögek között a jobb piramis:
1. Azt írja ide a háromszög alakú, ahol a szög ismeretlen.
2. A három betű S, A, O össze különböző pár. Kaptunk három szegmens.
3. Húzza ki az egyetlen, amely nem jellemző, hogy a háromszögek, amelyek ismert szögek.
4. Adjuk hozzá a levélben, hogy a név egy háromszög, amely egy ilyen szög:
5. Keresse a szegmens, amely a betűk közös.
6. Ahhoz, hogy megtalálja a szükséges függőség osztani a számláló és a nevező a talált szegmensben.
- Most, hogy ez emlékeztető eszköz, hozok kapcsolatát a szögek a jobb piramis.
1. A kapcsolat a síkja szöget a csúcsa a piramis és a megfelelő szögben a bázis szélén (négyszögletes gúla)
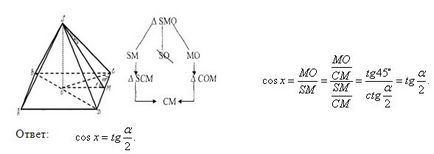
2. A kapcsolat a lapos szögben a jobb felső sarkában a piramis, és egy oldalsó széle
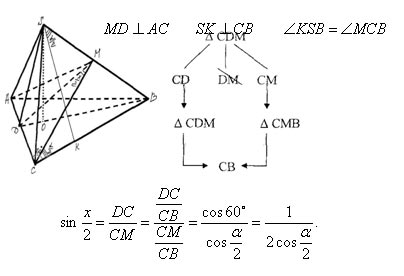
IV. Kialakulása az elsődleges képességek
Kedves 10-tiklassniki. Most, a gyakorlati munka, akkor meg fogja vizsgálni a kapcsolat a szögek a piramis a jobb, így minden csoport kap egy átmeneti képlet. Mindegyik csoportnak megvan a maga feladata. Ön az asztalra a feladatlapok <Приложение 2> és emlékezet <Приложение 3>. amely lehetővé teszi, hogy gyorsan megtalálja a szükséges függőségeket.
A diákok csoportokban dolgoznak. Végén egy reprezentatív általános képletű csoport teszi a kapott átmenetet a táblázatban a tárgylemezen.
Minden csoport jelent meg az asztalon jel piros lapot.<Приложение 4>Használja, akkor ellenőrizze a helyességét érvelés.

Ennek eredményeként a gyakorlati munka van egy tábla közötti kapcsolat szögek a jobb piramis. A következő lépés a mi bemutató, akkor használja ezeket a képleteket, hogy megoldja a problémákat, és ezzel egyidejűleg megbecsülni, hogy mennyi ilyen képletek megkönnyíti az életünket.
Térjünk vissza a probléma, hogy már megoldódott az elején a leckét. (A dia az oldattal és a függöny oldatot használva átmenet képletek)
Egy másik módja, hogy megoldja

Nyilvánvaló, hogy segítségével átmenet képletek nehézségek megoldásában problémák könnyen legyőzni. Van az asztalon egy tábla az átmeneti képletek <Приложение 5> nem csak a háromszög alakú és négyszögletes piramis, hanem hexagonális és n-szén. Ezek a képletek lehet és kell használni a problémák megoldásában.
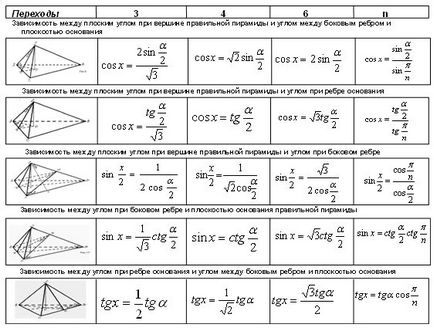
Tekintsük a képletek alkalmazásával egyéb feladatokat a tankönyv
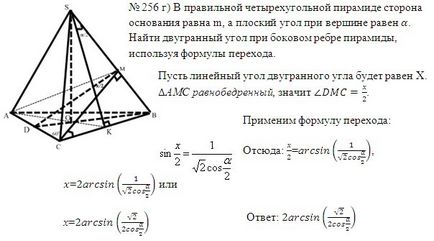
Azonban egy szép megoldás?
- Ma találkozott emlékeztető trükkök, hogy megtalálják a kapcsolat a szögek szabályos piramis, és használta egy emlékeztető eszköz egy pár ilyen függőségek, és alkalmazza őket, hogy megoldja a problémákat.
Megoldása komplex sztereometrikus problémák gyakran problémát okoz. Ezek különösen akkor állhat elő, mert a megadott adatok a lineáris elemek nem tartoznak azonos síkban, ezért nincs olyan derékszögű háromszöget, amellyel kezdeni a döntést. Azonban, a emlékezeterősítő eszközt, és mozgassa képletek nehézségek könnyen leküzdhetők.
Az ő munkája az értékelés, a következő leckét, a diákok ...
VII. házi feladat
Házi, azt javaslom, hogy megoldja a problémát 254 (b, d, e) két módja van: a hagyományos, és egy emlékeztető eszköz (átmeneti képlet).
- Köszönöm a leckét