A lejtőn a tangens, mint a lejtőn a CSE (2. oldal)
\ (\ Blacktriangleright \) Ha az egyenlet a vonal formájában adják \ (> \). száma \ (k \) nevezzük a lejtőn.
\ (\ Blacktriangleright \) szög \ (\ alpha \) egyenes meredeksége - közötti szög ebben egyenes vonal, és a pozitív irányban a tengely \ (Ox \) (\ (0 \ leqslant \ alpha<180^\circ\) ), лежащий в верхней полуплоскости.
\ (\ Blacktriangleright \) A alapvető képlet. A ferde vonal \ (y = kx + b \) meredeksége ennek egyenes:
\ [\, \ Alpha >>> \]
mert érintőleges grafikon - ez a közvetlen, akkor visszatér minden a vádakat.

Ha a \ (\ alpha<90^\circ\). то \(k>0 \);
ha a \ (\ alpha> 90 ^ \ circ \). a \ (k<0\) ;
ha a \ (\ alpha = 0 ^ \ circ \). a \ (k = 0 \) (egyenes egyenlete a következő formában \ (y = b \), és párhuzamos a tengellyel \ (Ox \));
ha a \ (\ alpha = 90 ^ \ circ \). a vonal egyenlet formájában \ (x = a \), és merőleges a tengelyre \ (Ox \).
Közvetlen \ (y = kx + 6 \) szöget zár \ (\ dfrac \) radiánban a negatív irányban a tengely \ (Ox \). Keresse meg a \ (k \).
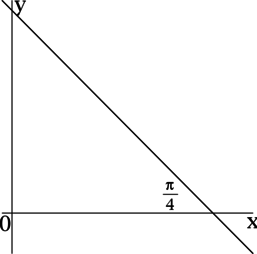
Az egyenes vonal a következő egyenlet adja \ (y = kx + b \). együttható \ (k \) az értéke az érintő közötti szög a vonal \ (y = kx + b \), és a pozitív irány a tengely \ (Ox \).
Mivel a szög közötti vonalat \ (y = kx + 6 \), és a negatív irányban a tengely \ (Ox \) egyenlő \ (\ dfrac \) radián közötti szög a vonal \ (y = kx + 6 \), és a pozitív tengely irányában \ (Ox \) egyenlő \ (\ pi - \ dfrac = \ dfrac \) radián, majd \ (k = \ mathrm \, \ dfrac = -1 \).
Find szög \ (\ alpha \) közötti egyenes vonal \ (y = \ sqrtx + 3 \ sqrt \) és a pozitív tengely irányában \ (Ox \). Válasz adni fok.
Az egyenes vonal a következő egyenlet adja \ (y = kx + b \). együttható \ (k \) az értéke az érintő közötti szög a vonal \ (y = kx + b \), és a pozitív irány a tengely \ (Ox \).
Így, \ (\ mathrm \, \ alpha = \ sqrt \). Mivel a mértéke intézkedés a szög két egyenes vonal közötti fekvő intervallumban \ ([0; 180 ^) \). és \ (\ mathrm \, \ alpha = \ sqrt> 0 \). A \ (0 <\alpha <\dfrac\). следовательно, \(\alpha = \mathrm\, (\sqrt) = \dfrac\). В итоге \(\alpha = 60^\) .
10. feladat = vizsga
Közvetlen \ (y = 21x - 6 \) szöget zár \ (\ alpha \) a pozitív tengely irányában \ (Ox \). és a vonal \ (y = -3x \) szöget zár \ (\ beta \) a pozitív tengely irányában \ (Ox \). Keresse meg a \ (\ mathrm \, \ alpha \ cdot \ mathrm \, \ beta \).
Az egyenes vonal a következő egyenlet adja \ (y = kx + b \). együttható \ (k \) az értéke az érintő közötti szög a vonal \ (y = kx + b \), és a pozitív irány a tengely \ (Ox \).
Így, \ (\ mathrm \, \ alpha = 21 \). és \ (\ mathrm \, \ beta = -3 \). Mivel a \ (\ mathrm \, \ beta \ neq 0 \). a \ (\ mathrm \, \ beta = \ dfrac \, \ beta> \). ahol \ (\ mathrm \, \ beta = - \ dfrac \). Összesen: \ (\ mathrm \, \ alpha \ cdot \ mathrm \, \ beta = 21 \ cdot \ left (- \ dfrac \ right) = -7 \).
Beállítása 11 = vizsga
Az egyenes vonal a következő egyenlet adja \ (y = 3x + 2 \). Ami a grafika néhány függvény \ (f (x) \) azon a ponton, \ ((x_0; f (x_0)) \). és a vonal \ (y = 6x + 4 \) a grafikákat ugyanazt a funkciót a ponton \ ((x_1; f (x_1)) \).
Keresse meg az összeget az érintők dőlésszöge az érintő a grafikon \ (f (x) \) a pontokon \ ((x_0 f (x_0)) \) és \ ((x_1 f (x_1)) \). ahol a dőlésszög tekintjük közötti szögben az egyenes vonal és a pozitív irányba \ (Ox \).
Az egyenes vonal a következő egyenlet adja \ (y = kx + b \). együttható \ (k \) az értéke az érintő közötti szög a vonal \ (y = kx + b \), és a pozitív irány a tengely \ (Ox \).
Így, közvetlen \ (y = 3x + 2 \) kívánt meredeksége egyenlő a \ (3 \). és a közvetlen \ (y = 6x + 4 \) a lejtőn a kívánt szög \ (6 \). Összesen: összege érintők a dőlésszöge az érintő a grafikon \ (f (x) \) a pontokon \ ((x_0 f (x_0)) \) és \ ((x_1 f (x_1)) \) a \ (9 \ ).
Beállítása 12 = vizsga