A legnagyobb és a legkisebb érték a függvény
Gyakorlati szempontból a legérdekesebb a származékos ügyletekre annak érdekében, hogy megtalálják a legnagyobb és legkisebb értéket a függvény. Mi ennek az oka? Profitmaximalizálás, költségminimalizálás meghatározzuk az optimális kihasználását berendezés. Más szóval, az élet számos területén szükség van, hogy megoldja a problémát, optimalizálása minden paramétert. És ez a probléma megtalálni a legnagyobb és legkisebb értéket a függvény.
Meg kell jegyezni, hogy a legnagyobb és a legkisebb érték a funkciót szánnak jellemzően egy intervallum X. amely egy egész vagy függvény értelmezési tartománya vagy része a domain meghatározás. Self intervallum X lehet egy szegmens nyílt intervallum végtelen intervallum.
Ebben a cikkben fogunk beszélni megtalálni a maximális és minimális értékei explicit függvénye egyváltozós y = f (x).
Oldalnavigáció.
A legnagyobb és a legkisebb érték a funkció - meghatározás, illusztrálja.
Röviden megvitassák az alapvető definíciókat.
A legmagasabb érték a függvény y = f (x) intervallumban X nevezzük értéket úgy, hogy minden egyenlőtlenség.
A legkisebb érték a függvény y = f (x) intervallumban X nevezzük értéket úgy, hogy minden egyenlőtlenség.
Ezek a definíciók intuitív: a legnagyobb (legkisebb) függvény értékét - ez a legnagyobb (legkisebb) értéke érkezett az intervallumot, az abszcissza.
A stacionárius pontok - azok az értékek, az érvelés, amelyben a származék lesz nulla.
Miért fix pont, amikor a maximális és minimális értékeket? A válasz erre a kérdésre adott Fermat-tétel. Ebből következik, hogy ha a tétel differenciálható függvény egy szélsőérték (helyi minimum vagy helyi maximum) egy bizonyos ponton, akkor ezen a ponton van rögzítve. Tehát a függvény gyakran vesz el maximumát (minimum) érték az intervallumon X az egyik fix pontok ezen az intervallumon.
Ugyancsak gyakran a legnagyobb és a legkisebb érték a funkció lehet hozni a pontokat, ahol ott van az első származék ezt a funkciót, és a funkció határozza meg.
Azonnal a válasz az egyik leggyakoribb kérdés, a témáról: „Ez mindig meg lehet határozni a legmagasabb (legalacsonyabb) függvény értékét”? Nem, nem mindig. Előfordul, hogy a határ intervallum X egybeesnek a határait terén meghatározása a függvény vagy az intervallum X végtelen. És néhány funkció a végtelenben és a határok mezőmeghatározásainak lehet venni, mint végtelenül nagy és a végtelenül kicsi értékeket. Ezekben az esetekben nem lehet elmondani a legmagasabb és a legalacsonyabb érték a funkciót.
Az egyértelműség kedvéért, adunk egy grafikus ábrázolása. Nézd meg a számok - és sokkal tisztább.
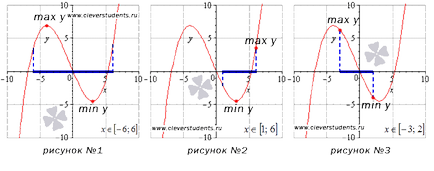
Az első kép függvény a legmagasabb (maximum y) és a legkisebb (min y) értékek stacionárius pontok, amelyek belsejében az intervallum [-6, 6].
Vegyük azt az esetet mutatja, a második képen. Változás a szegmens [1, 6]. Ebben a példában a legkisebb értéket elért egy fix pont, és a legnagyobb - a lényeg az abszcissza megfelelő jobb szélét az intervallum.
Ábra №3 határpontok intervallum [-3, 2] az abszcisszán pontok megfelelő a legnagyobb és a legkisebb a függvény értékét.
A nyílt intervallum
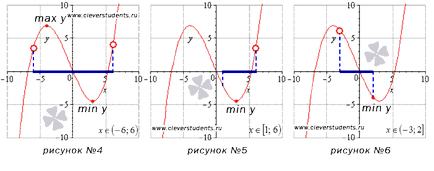
A negyedik képen függvény a legmagasabb (max y) és a legkisebb (min y) értékeket a stacionárius pontok belül található nyílt intervallumot (-6, 6).
Az intervallum [1, 6) a legkisebb érték a funkciót is elérhetünk egy állandó ponton, és a legnagyobb érték nem tudunk mondani semmit. Ha az x = 6 része volt az intervallum, mivel ha ez a függvény értékét venné a legnagyobb értéket. Ez a példa ábrán látható №5.
Ábra №6 legkisebb érték elérte a megfelelő határán intervallum (-3 ;. 2] a legnagyobb érték minden következtetéseket lehet levonni.
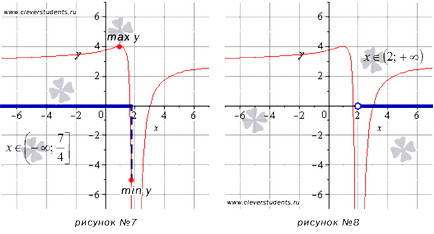
A bemutatott példában a hetedik ábrán, a függvény a legmagasabb érték (max y) egy helyhez kötött ponton abszcissza x = 1. és a legkisebb érték (min y) érjük el a jobb határán az intervallumban. Abban értékek mínusz végtelen aszimptotikusan közelít y = 3.
Az intervallum funkció nem éri el a legkisebb vagy a legnagyobb érték. Törekvés során az x = 2 Jobb funkció értékek általában mínusz végtelen (egyenes x = 2 egy függőleges aszimptőta), és az abszcissza hajlamos plusz végtelenig, a függvény értékei aszimptotikusan közelít y = 3. Grafikus ábrázolása ebben a példában ábrán látható №8.
Az algoritmus megtalálása a legnagyobb és a legkisebb érték folytonos függvény az intervallumon [a; b].
Írunk az algoritmus megtalálása a legnagyobb és a legkisebb érték a függvény az intervallumon.
- Keresse meg a domain a funkció, és ellenőrzi, hogy a teljes intervallum [a; b].
- Összes pont, ahol nem áll az első derivált és amely tartalmazza az intervallum [a; b] (általában ilyen pontok vstechayutsya funkció egy érv a modulusz megjelölés és teljesítmény funkciókat frakcionált-racionális indikátor). Ha ezek a pontok nem rendelkeznek, akkor megyünk tovább a következő lépésre.
- Határozzuk meg az összes stacionárius pont alá tartozó, az [a; b]. Ehhez találunk a függvény deriváltját. egyenlőségjelet nullára, és megoldani a kapott egyenlet válassza ki a megfelelő gyökér. Ha nincs stacionárius pont, vagy egyikük sem éri el a vágás, akkor folytassa a következő lépéssel.
- Kiszámoljuk a függvény értékei a kiválasztott fixpontok (ha van ilyen) a pontok, ahol nincs első származékot (ha van ilyen), és ha x = a és x = b.
- A kapott értékek a funkciót, válassza a legnagyobb és a legkisebb - ezek a kívánt legmagasabb és a legalacsonyabb érték a függvény volt.
Nézzük az algoritmus megoldására példát találni a legnagyobb és a legkisebb érték az intervallum.
Keresse meg a legnagyobb és a legkisebb érték a függvény- intervallumban [1; 4];
- intervallumban [-4, -1].
Kezdjük a domain a funkciót. Másodfokú polinom a nevezőben nem vész el:

Ez könnyen ellenőrizhető, hogy minden időközönként a feltételeket, a probléma tartozik a domain a funkciót.
Nyilvánvaló, hogy a származékos létezik az egész tartomány a funkciót.
Mi található a stacionárius pontok. Származtatott eltűnik címen. Ez a stacionárius pont esik a időközönként (-3, 1] és (-3, 2).
Egy első időszak kiszámításához a függvény értéke az x = -4, és egy határ a mínusz végtelen:
Azóta és a legkevésbé a függvény a következtetést lehet levonni. Az ember csak azt mondják, hogy a függvény értékek határolt alábbiakban értéke -1 (mínusz végtelen függvény értéke aszimptotikusan közelít egy egyenes vonal y = -1).
A második intervallum az érdeklődés, amely nem tartalmaz minden olyan helyhez kötött pont, és egyik sem nem szigorú határokat. Ebben az esetben nem találunk a legnagyobb vagy legkisebb érték a funkciót. Kiszámítása a határ mínusz végtelen és az argumentum általában mínusz három, a bal oldalon, csak akkor lesz képes meghatározni a tartományban az értékek:
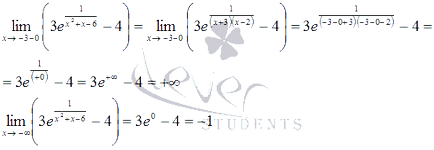
Következésképpen, a függvény értékei vannak a tartományban található x rés.
A harmadik szakasz (-3, 1] értékének kiszámításához az a funkció az álló ponton, és amikor X = 1 és egyoldalú limit, az érvelés hajlamos -3 jobbra :.
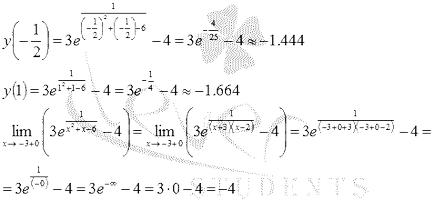
Következésképpen a legnagyobb értéke ebben az intervallumban a függvény stacionárius pont, a legkisebb érték a függvény, nem tudjuk kiszámítani, de az értéket a funkció csak alulról -4.
Az intervallum (-3, 2) az eredmények az előző bekezdésben és a további kiszámítja kétoldalas határa hajlamos Deuce balra:
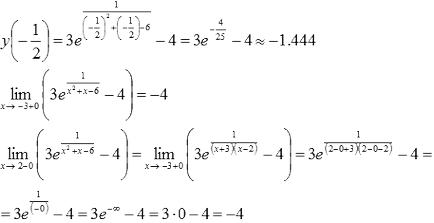
Ezért a legkisebb érték nem állapítható meg, az értékek a funkciók csak alulról -4.
Az eredmények az előző két pont azt sugallják, hogy az intervallum [1; 2) kapja a legnagyobb értéket a függvény az x = 1. a legkisebb érték nem található, az értékek a funkciók csak alulról -4.
Az intervallum funkció nem érte el a legnagyobb vagy a legkisebb érték.
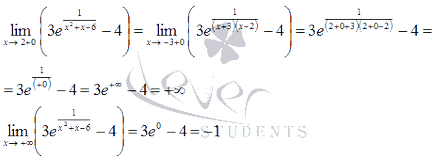
Azaz, ebben a tartományban vesz értékek közötti intervallumban.
Értékének kiszámításánál a függvény x = 4. azt lehet mondani, hogy a plusz végtelenben funkciót aszimptotikusan közelít egy egyenes vonal y = -1.
Most lehet összehasonlítani a kapott eredményeket minden pontján a függvény grafikonját. Kék szaggatott vonalak jelzik a asymptote.
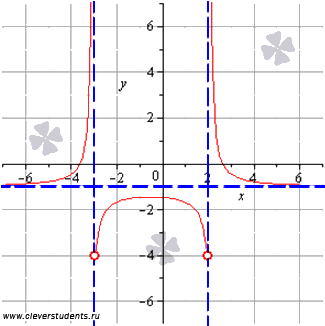
Ezen akkor a végén megtalálni a legnagyobb és legkisebb értéket a függvény. Az algoritmusok megérteni ezt a cikket, hogy eredményeket lehessen elérni minimális hatásával. Azonban célszerű először meghatározzák a időközönként növekedése és csökkenése a funkció, és csak ezután következtetéseket levonni a legmagasabb és a legalacsonyabb érték a függvény minden intervallumban. Ez ad egy tisztább képet és a szigorú igazolása az eredményeket.