A grafikus megoldási módja az egyenletek az algoritmus és példák a grafikonok
legfontosabb nbsp> nbsp Wiki-bemutató nbsp> nbsp Matematika nbsp> nbsp8 osztály nbsp> nbspGrafichesky módon megoldani az egyenleteket: egy algoritmus és a minta menetrendek
Egy módon oldja meg a egyenletek grafikus módon. Ez alapján az ábrázolási funkciók és okaik metszéspontjai. Tekintsük a grafikus megoldási módja másodfokú egyenlet a * x ^ 2 + b * x + c = 0.
Az első módszer, hogy megoldja
Mi átalakítani az egyenlet a * x ^ 2 + b * x + c = 0 a formában a * x ^ 2 = -B * X-C. Plot grafikonok két függvény az y = a * x ^ 2 (parabola) és y = -b * X-C (direkt). Keresünk metszéspontján. Az abszcissza a metszéspontok és lesz a megoldása az egyenletnek.
Megmutatjuk egy példát: az egyenlet megoldásához x ^ 2-2 * X-3 = 0.
Mi átalakítja azt x ^ 2 = 2 * x + 3. Készítünk egy koordináta rendszerben grafikonok függvény az y = x ^ 2 és y = 2 * x + 3.
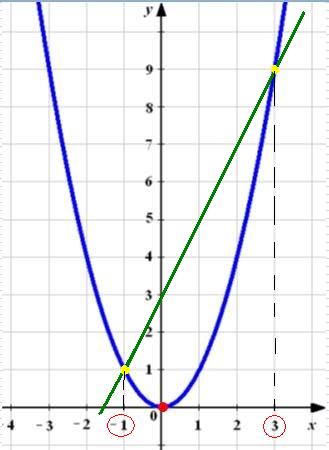
A grafikonok metszi a két pontot. Az abszcissza lesz a gyökerei az egyenlet.
A döntés, amelyet a képlet
Annak ellenőrzésére, hogy hiteles-e megoldás analitikusan. Nézzük megoldani a másodfokú egyenlet képlet szerint:
Tehát megoldás ugyanaz.
Grafikus módszer egyenletek megoldására van egy hátránya, segítségével ez nem mindig lehetséges egzakt megoldása az egyenletnek. Próbáljuk megoldani az egyenletet x ^ 2 = 3 + x.
Készítünk egyetlen koordináta-rendszerben, a parabola y = x ^ 2 és y = 3 + x.
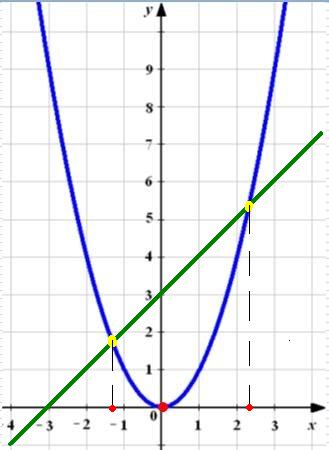
Ismét kapott egy hasonló mintázatot. Közvetlen parabola és metszik a két pontot. De a pontos értéket az abszcissza a ponton már nem lehet azt mondani, csak közelítő: x≈-1,3 x≈2,3.
Ha elégedettek vagyunk a választ, mint a pontosság, akkor lehetséges, hogy használja ezt a módszert, de ez ritkán fordul elő. Általában pontos megoldásokra van szükség. Ezért a grafikus módszer csak ritkán, főleg ellenőrzésére meglévő megoldásokat.